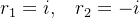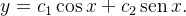5.5 Equações diferenciais com coeficientes constantes
Na equação diferencial (5.14) se fazemos 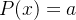 ,
, 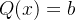 ,
, 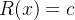 e
e 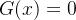 , com
, com 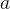 ,
, 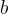 e
e  constantes reais então ela se transforma na seguinte equação:
constantes reais então ela se transforma na seguinte equação:
| |
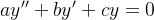 |
|
(5.18) |
É natural considerar uma solução de (5.18) na forma:
| |
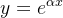 |
|
(5.19) |
com 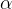 sendo uma constante a determinar. Derivando
sendo uma constante a determinar. Derivando 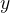 dada por (5.19) em relação a
dada por (5.19) em relação a  , temos
, temos
Substituindo os valores de 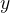 ,
, 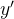 e
e 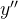 em (5.18) obtemos:
em (5.18) obtemos:
que resulta na seguinte igualdade:
Como 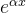 é sempre diferente, devemos ter que:
é sempre diferente, devemos ter que:
| |
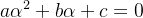 |
|
(5.20) |
A equação (5.20) é conhecida como equação caracter stica associada à equação (5.18). Temos então três casos a considerar: as ra
stica associada à equação (5.18). Temos então três casos a considerar: as ra zes
zes 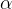 de (5.20) são reais e distintas, elas são reais e iguais ou são complexas conjugadas. Quando forem reais e distintas, isto é,
de (5.20) são reais e distintas, elas são reais e iguais ou são complexas conjugadas. Quando forem reais e distintas, isto é, 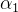 e
e 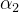 satisfazendo a equação (5.20) então temos duas soluções linearmente independentes da equação (5.18), dadas por:
satisfazendo a equação (5.20) então temos duas soluções linearmente independentes da equação (5.18), dadas por:
Essas duas soluções formam um conjunto fundamental de soluções da equação (5.18) e, portanto, a solução geral dessa equação é dada pela combinação linear dessas duas soluções, ou seja, 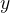 dada por
dada por
| |
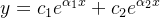 |
|
(5.21) |
com 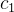 e
e 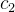 constantes arbitrárias, é a solução geral da equação (5.18). Se as raízes forem iguais, isto é,
constantes arbitrárias, é a solução geral da equação (5.18). Se as raízes forem iguais, isto é,  então uma solução é da forma
então uma solução é da forma 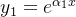 e a outra solução linearmente independente com essa é dada por
e a outra solução linearmente independente com essa é dada por 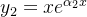 que é encontrada usando o método de variação dos parâmetros. Logo a solução geral da equação (5.18) nesse caso, é dada por:
que é encontrada usando o método de variação dos parâmetros. Logo a solução geral da equação (5.18) nesse caso, é dada por:
| |
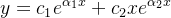 |
|
(5.22) |
com 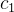 e
e 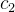 constantes arbitrárias. No caso complexo, uma das ra
constantes arbitrárias. No caso complexo, uma das ra zes sendo da forma
zes sendo da forma 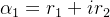 uma solução complexa é da forma
uma solução complexa é da forma
| |
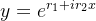 |
|
(5.23) |
Se queremos as duas soluções reais linearmente independentes da equação (5.18), para esse caso, basta tomar 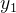 como sendo a parte real de (5.23) e
como sendo a parte real de (5.23) e 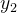 como sendo a parte imaginária (5.23), ou seja,
como sendo a parte imaginária (5.23), ou seja,
| |
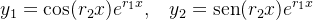 |
|
(5.24) |
E a solução geral de (5.18) é dada por
| |
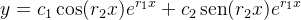 |
|
(5.25) |
com 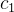 e
e 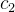 constantes arbitrárias. Quando estamos resolvendo uma equação diferencial do tipo (5.18) satisfazendo condições iniciais então podemos determinar as constantes
constantes arbitrárias. Quando estamos resolvendo uma equação diferencial do tipo (5.18) satisfazendo condições iniciais então podemos determinar as constantes 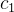 e
e 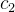 , ou seja, elas deixam de ser arbitrárias.
, ou seja, elas deixam de ser arbitrárias.
Example 115. Considere a equação diferencial
| |
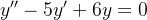 |
|
(5.26) |
com os dados iniciais dados por
| |
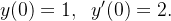 |
|
(5.27) |
A equação caracter stica associada à equação (5.26) é dada por
stica associada à equação (5.26) é dada por
| |
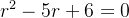 |
|
(5.28) |
cujas ra zes são
zes são
| |
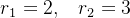 |
|
(5.29) |
Logo a solução geral de (5.26) é
| |
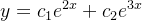 |
|
(5.30) |
Como queremos que essa solução satisfaça as condições iniciais (5.27) devemos ter: resolvendo o sistema acima, obtemos, 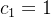 e
e 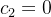 . Logo, a única solução da equação (5.26) que satisfaz as condições iniciais (5.27) é
. Logo, a única solução da equação (5.26) que satisfaz as condições iniciais (5.27) é 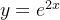 .
.
Example 116. Considere a equação diferencial
| |
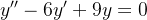 |
|
(5.31) |
A equação caracter stica associada à equação (5.31) é dada por
stica associada à equação (5.31) é dada por
| |
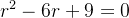 |
|
(5.32) |
cuja ra z é
z é
| |
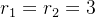 |
|
(5.33) |
Logo a solução geral de (5.31) é
| |
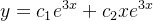 |
|
(5.34) |
Example 117. Considere a equação diferencial
| |
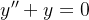 |
|
(5.35) |
A equação caracter stica associada à equação (5.35) é dada por
stica associada à equação (5.35) é dada por
| |
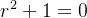 |
|
(5.36) |
cujas ra zes complexas são
zes complexas são
| |
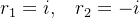 |
|
(5.37) |
Logo a solução geral de (5.35) é
| |
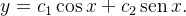 |
|
(5.38) |
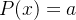 ,
, 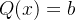 ,
, 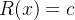 e
e 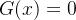 , com
, com 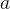 ,
, 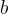 e
e  constantes reais então ela se transforma na seguinte equação:
constantes reais então ela se transforma na seguinte equação: 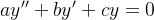
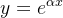
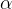 sendo uma constante a determinar. Derivando
sendo uma constante a determinar. Derivando 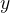 dada por (5.19) em relação a
dada por (5.19) em relação a  , temos
, temos 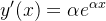
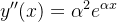
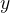 ,
, 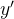 e
e 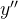 em (5.18) obtemos:
em (5.18) obtemos: ![\[ a \alpha ^2 e^{\alpha x}+b \alpha e^{\alpha x}+ ce^{\alpha x}=0 \]](images/img-1050.png)
![\[ (a \alpha ^2 +b \alpha + c)e^{\alpha x}=0 \]](images/img-1051.png)
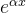 é sempre diferente, devemos ter que:
é sempre diferente, devemos ter que: 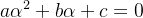
 stica associada à equação (5.18). Temos então três casos a considerar: as ra
stica associada à equação (5.18). Temos então três casos a considerar: as ra zes
zes 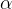 de (5.20) são reais e distintas, elas são reais e iguais ou são complexas conjugadas. Quando forem reais e distintas, isto é,
de (5.20) são reais e distintas, elas são reais e iguais ou são complexas conjugadas. Quando forem reais e distintas, isto é, 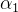 e
e 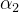 satisfazendo a equação (5.20) então temos duas soluções linearmente independentes da equação (5.18), dadas por:
satisfazendo a equação (5.20) então temos duas soluções linearmente independentes da equação (5.18), dadas por: 
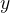 dada por
dada por 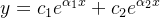
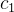 e
e 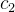 constantes arbitrárias, é a solução geral da equação (5.18). Se as raízes forem iguais, isto é,
constantes arbitrárias, é a solução geral da equação (5.18). Se as raízes forem iguais, isto é,  então uma solução é da forma
então uma solução é da forma 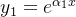 e a outra solução linearmente independente com essa é dada por
e a outra solução linearmente independente com essa é dada por 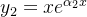 que é encontrada usando o método de variação dos parâmetros. Logo a solução geral da equação (5.18) nesse caso, é dada por:
que é encontrada usando o método de variação dos parâmetros. Logo a solução geral da equação (5.18) nesse caso, é dada por: 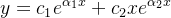
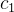 e
e 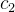 constantes arbitrárias. No caso complexo, uma das ra
constantes arbitrárias. No caso complexo, uma das ra zes sendo da forma
zes sendo da forma 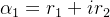 uma solução complexa é da forma
uma solução complexa é da forma 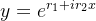
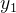 como sendo a parte real de (5.23) e
como sendo a parte real de (5.23) e 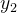 como sendo a parte imaginária (5.23), ou seja,
como sendo a parte imaginária (5.23), ou seja, 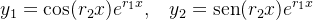
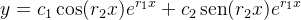
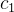 e
e 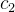 constantes arbitrárias. Quando estamos resolvendo uma equação diferencial do tipo (5.18) satisfazendo condições iniciais então podemos determinar as constantes
constantes arbitrárias. Quando estamos resolvendo uma equação diferencial do tipo (5.18) satisfazendo condições iniciais então podemos determinar as constantes 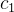 e
e 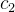 , ou seja, elas deixam de ser arbitrárias.
, ou seja, elas deixam de ser arbitrárias. 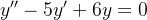
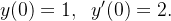
 stica associada à equação (5.26) é dada por
stica associada à equação (5.26) é dada por 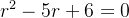
 zes são
zes são 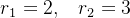
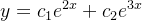
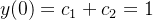
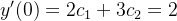
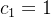 e
e 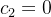 . Logo, a única solução da equação (5.26) que satisfaz as condições iniciais (5.27) é
. Logo, a única solução da equação (5.26) que satisfaz as condições iniciais (5.27) é 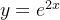 .
. 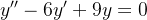
 stica associada à equação (5.31) é dada por
stica associada à equação (5.31) é dada por 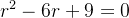
 z é
z é 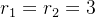
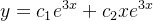
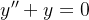
 stica associada à equação (5.35) é dada por
stica associada à equação (5.35) é dada por 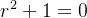
 zes complexas são
zes complexas são