| Séries e Equações Diferenciais Ordinárias |
 cios
ciosResolva as seguintes equações diferenciais lineares com condições iniciais dadas:
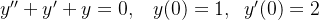 .
.
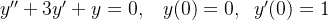 .
.
Encontre a solução geral das equações diferenciais abaixo:
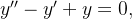
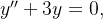
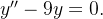
Mostre que as equações abaixo tem duas soluções linearmente independentes e calcule o Wronskiano de cada uma delas:
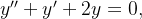
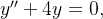
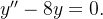
Considere o problema não homogêneo abaixo:
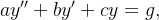 |
(5.39) |
onde 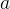 ,
, 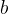 ,
,  e
e 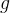 são funções de
são funções de 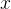 diferenciáveis. Suponha que
diferenciáveis. Suponha que 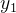 e
e 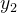 são soluções linearmente independentes do problema homogêneo associado ao problema (5.39):
são soluções linearmente independentes do problema homogêneo associado ao problema (5.39):
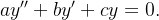 |
(5.40) |
Considere uma solução particular de (5.39) dada por
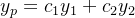 |
(5.41) |
onde 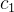 e
e 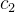 são funções de
são funções de 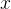 . Use o método de variação dos parâmetros para encontrar uma solução particular
. Use o método de variação dos parâmetros para encontrar uma solução particular 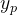 de (5.39). Ou seja, suponha que
de (5.39). Ou seja, suponha que 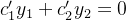 , derive (5.41) para obter
, derive (5.41) para obter 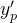 e
e 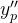 substitua esses valores em (5.39) para obter o sistema
substitua esses valores em (5.39) para obter o sistema
![\begin{equation} \left\{ \begin{array}[l]cc^{\prime }_1 y_1+c^{\prime }_2 y_2=0\\ c^{\prime }_1 y^{\prime }_1+c^{\prime }_2 y^{\prime }_2=\dfrac {g}{a} \end{array}\right.\label{exerc4} \end{equation}](images/img-1103.png) |
(5.42) |
Resolva esse sistema para 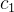 e
e 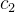 e encontre a solução particular
e encontre a solução particular 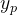 dada por (5.41) onde
dada por (5.41) onde 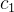 e
e 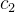 são soluções de (5.42). Logo a solução geral do problema (5.39) é dada por
são soluções de (5.42). Logo a solução geral do problema (5.39) é dada por
![\[ y(x)=y_ p(x)+c_1 y_1(x)+c_2 y_2(x) \]](images/img-1104.png) |
onde 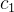 e
e 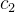 são constantes arbitrárias.
são constantes arbitrárias.
Aplique o método de variação dos parâmetros do exerc cio anterior para determinar a solução geral dos problemas não homogêneos abaixo:
cio anterior para determinar a solução geral dos problemas não homogêneos abaixo: