| Séries e Equações Diferenciais Ordinárias |
A equação
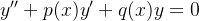 |
(5.16) |
é a equação homogênea associada à equação (5.15).
Theorem 114. Se 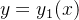 e
e 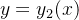 são soluções da equação diferencial (5.16) então
são soluções da equação diferencial (5.16) então 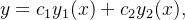 (
(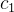 e
e 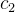 constantes arbitrárias) é também solução de (5.16).
constantes arbitrárias) é também solução de (5.16).
Duas soluções 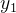 e
e 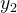 de (5.16) formarão um conjunto fundamental de soluções se toda solução de (5.16) puder ser escrita como combinação linear de
de (5.16) formarão um conjunto fundamental de soluções se toda solução de (5.16) puder ser escrita como combinação linear de 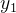 e
e 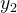 . O Wronskiano de
. O Wronskiano de 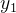 e
e 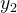 é dado por
é dado por
![\begin{equation} W(y_{1},y_{2})=\left\vert \begin{array}[c]{cc}y_{1} & y_{2}\\ y_{1}^{\prime } & y_{2}^{\prime }\end{array} \right\vert =y_{1}y_{2}^{\prime }-y_{2}y_{1}^{\prime }\end{equation}](images/img-1037.png) |
(5.17) |
se 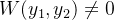 então
então 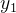 e
e 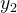 formam um conjunto fundamental de solução de (5.16). Isto quer dizer que as soluções
formam um conjunto fundamental de solução de (5.16). Isto quer dizer que as soluções 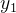 e
e 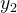 são linearmente independentes e toda solução de (5.16) se escreve como combinação linear dessas duas soluções.
são linearmente independentes e toda solução de (5.16) se escreve como combinação linear dessas duas soluções.