| Séries e Equações Diferenciais Ordinárias |
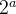 Ordem
OrdemUma equação diferencial de 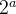 ordem, na forma mais geral, é uma equação do tipo
ordem, na forma mais geral, é uma equação do tipo
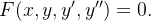 |
(5.11) |
onde 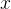 é a variável independente, e
é a variável independente, e 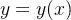 é a variável dependente, aqui
é a variável dependente, aqui 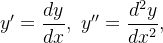
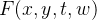 é uma função dada. Em muitas situações de muitos problemas de aplicações (na f
é uma função dada. Em muitas situações de muitos problemas de aplicações (na f sica, na matemática, etc.) a equação (5.11) se apresenta na seguinte forma
sica, na matemática, etc.) a equação (5.11) se apresenta na seguinte forma
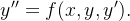 |
(5.12) |
Theorem 110. Se as funções 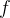 ,
, 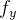 e
e 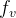 são cont
são cont nuas numa região aberta
nuas numa região aberta 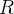 do espaço tri-dimensional
do espaço tri-dimensional 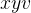 e se o ponto
e se o ponto 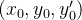 está em
está em 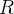 , então em algum intervalo em torno de
, então em algum intervalo em torno de 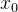 , existe uma única solução
, existe uma única solução 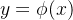 da equação diferencial (5.12) que satisfaz as condições iniciais
da equação diferencial (5.12) que satisfaz as condições iniciais
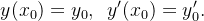
(5.13)
A equação geral linear de segunda ordem pode ser dada no seguinte modo
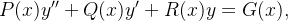 |
(5.14) |
onde 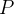 ,
, 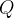 ,
, 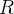 e
e  são funções dadas.
são funções dadas.
Example 111. Equação de Legendre de ordem 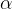
![\[ (1-x^{2})y^{\prime \prime }-2xy^{\prime }+\alpha (\alpha +1)y=0 \]](images/img-1022.png)
Example 112. Equação de Bessel de ordem 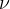
![\[ x^{2}y^{\prime \prime }+xy^{\prime }+(x^{2}-\nu ^{2})y=0. \]](images/img-1024.png)
Supondo 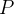 ,
, 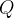 ,
, 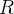 e
e  cont
cont nuas num certo intervalo
nuas num certo intervalo 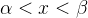 , e que
, e que 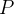 nunca se anula no intervalo, podemos dividir a equação (5.14) por
nunca se anula no intervalo, podemos dividir a equação (5.14) por 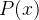 e obter uma equação da forma
e obter uma equação da forma
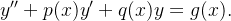 |
(5.15) |
Theorem 113. Se as funções 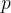 ,
, 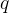 e
e 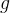 são cont
são cont nuas num intervalo
nuas num intervalo 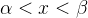 , então existe uma e somente uma função
, então existe uma e somente uma função 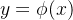 que satisfaz a equação diferencial (5.15) e as condições iniciais (5.13).
que satisfaz a equação diferencial (5.15) e as condições iniciais (5.13).