| Cálculo Diferencial e Integral 3 |
Seja  uma função contínua definida numa região
uma função contínua definida numa região 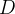 do plano-xy que contém a curva suave
do plano-xy que contém a curva suave 
Particionando o intervalo ![$[a,b]$](images/img-0666.png)
![\[ a=t_{0}<t_{1}<\cdots <t_{n}=b \]](images/img-0667.png) |
Denotemos por  a norma desta partição. Se
a norma desta partição. Se  é o ponto em
é o ponto em  correspondente a
correspondente a  então os pontos
então os pontos 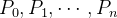 dividem
dividem  em
em 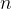 partes
partes 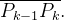 Seja
Seja
![\[ \Delta x_{k}=x_{k}-x_{k-1},\ \ \Delta y_{k}=y_{k}-y_{k-1},\ \ \Delta s_{k}=\text { comprimento de }\overline{P_{k-1}P_{k}} \]](images/img-0673.png) |
Para cada 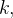 seja
seja  um ponto em
um ponto em 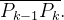 Consideremos os três seguintes somatórios
Consideremos os três seguintes somatórios
![\[ \sum _{k}f(u_{k},v_{k})\Delta s_{k},\ \ \sum _{k}f(u_{k},v_{k})\Delta x_{k},\ \ \sum _{k}f(u_{k},v_{k})\Delta y_{k} \]](images/img-0676.png) |
Definimos as integrais curvilíneas se os limites existirem
 |
(4) |
 |
(5) |
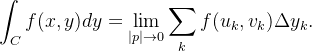 |
(6) |
Se  é contínua em
é contínua em 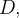 então os limites em
então os limites em  e
e 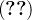 existem e são os mesmos para toda parametrização de
existem e são os mesmos para toda parametrização de  (desde que se adote a mesma orientação). Usando a parametrização de
(desde que se adote a mesma orientação). Usando a parametrização de 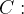
 temos
temos
![\[ dx=\alpha ^{\prime }(t)dt,\ \ dy=\beta ^{\prime }(t),\ ds=\sqrt{\left( dx\right) ^{2}+\left( dy\right) ^{2}}=\sqrt{\left( \alpha ^{\prime }(t)\right) ^{2}+\left( \beta ^{\prime }(t)\right) ^{2}}dt \]](images/img-0685.png) |
Temos então o resultado.
Se uma curva suave  é dada por
é dada por 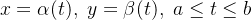 e se
e se  é contínua numa região
é contínua numa região 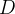 contendo
contendo 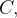 então
então
![\[ \int _{C}f(x,y)ds=\int _{a}^{b}f(\alpha (t),\beta (t))\sqrt{\left( \alpha ^{\prime }(t)\right) ^{2}+\left( \beta ^{\prime }(t)\right) ^{2}}dt \]](images/img-0689.png) |
![\[ \int _{C}f(x,y)dx=\int _{a}^{b}f(\alpha (t),\beta (t))\alpha ^{\prime }(t)dt \]](images/img-0690.png) |
![\[ \int _{C}f(x,y)dy=\int _{a}^{b}f(\alpha (t),\beta (t))\beta ^{\prime }(t)dt. \]](images/img-0691.png) |
Tal resultado pode ser extendido para curvas parcialmente suaves, isto é, se
![\[ C=C_{1}\cup C_{2}\cup \cdots \cup C_{n} \]](images/img-0692.png) |
então
![\[ \int _{C}f(x,y)ds=\int _{C_{1}}f(x,y)ds+\int _{C_{2}}f(x,y)ds+\cdots +\int _{C_{n}}f(x,y)ds. \]](images/img-0693.png) |
Também
![\[ \int _{C}f(x,y)ds=-\int _{-C}f(x,y)ds \]](images/img-0694.png) |
e
![\[ \int _{C}\left( f(x,y)+g\left( x,y\right) \right) ds=\int _{C}f(x,y)ds+\int _{C}g(x,y)ds. \]](images/img-0695.png) |
Calcule 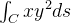 se
se  admite a parametrização
admite a parametrização
![\[ x=\cos t,\ y=\operatorname {sen}t,\ 0\leq t\leq \frac{\pi }{2}. \]](images/img-0697.png) |
Aplicando o Teorema obtemos
![\[ \int _{C}xy^{2}ds=\int _{0}^{\frac{\pi }{2}}\cos t\left( \operatorname {sen}^{2}t\right) \sqrt{\operatorname {sen}^{2}t+\cos ^{2}t}dt=\int _{0}^{\frac{\pi }{2}}\left( \operatorname {sen}^{2}t\right) \cos t\ dt=\frac{1}{3}. \]](images/img-0698.png) |
Calcule 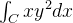 e
e 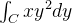 se
se  é a parte da parábola
é a parte da parábola 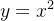 de
de 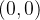 a
a 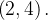
As equações paramétricas de  são
são
![\[ x=t,\ y=t^{2},\ 0\leq t\leq 2 \]](images/img-0704.png) |
As diferenciais são
![\[ dx=dt,\ dy=2tdt \]](images/img-0705.png) |
assim
![\[ \int _{C}xy^{2}dx=\int _{0}^{2}t(t^{2})^{2}dt=\int _{0}^{2}t^{5}dt=\left[ \frac{t^{6}}{6}\right] _{0}^{2}=\frac{32}{3}, \]](images/img-0706.png) |
![\[ \int _{C}xy^{2}dy=\int _{0}^{2}t\left( t^{2}\right) ^{2}2tdt=2\int _{0}^{2}t^{6}dt=\frac{2}{7}\left[ t^{7}\right] _{0}^{2}=\frac{256}{7}. \]](images/img-0707.png) |
Podiamos ter feito: 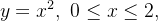 assim
assim 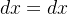 e
e 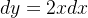
![\[ \int _{C}xy^{2}dx=\int _{0}^{2}x\left( x^{2}\right) ^{2}dx=\int _{0}^{2}x^{5}dx=\frac{32}{3} \]](images/img-0711.png) |
![\[ \int _{C}xy^{2}dy=\int _{0}^{2}x\left( x^{2}\right) ^{2}2xdx=2\int _{0}^{2}x^{6}dx=\frac{256}{7}. \]](images/img-0712.png) |
Considere a função vetorial 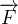 com domínio
com domínio 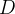 onde a curva
onde a curva 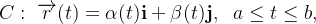 está inserida. Definimos
está inserida. Definimos
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{a}^{b}\overrightarrow {F}(\overrightarrow {r}(t))\cdot \overrightarrow {r}^{\prime }(t)\ dt \]](images/img-0714.png) |
em outras palavras podemos dizer que se 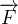
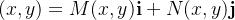
 e
e 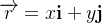 então
então
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{C}M(x,y)dx+N(x,y)dy. \]](images/img-0717.png) |
Se 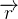 e
e 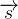 representam dois caminhos equivalentes e regulares então
representam dois caminhos equivalentes e regulares então
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{C}\overrightarrow {F}\cdot d\overrightarrow {s} \]](images/img-0720.png) |
sempre que 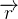 e
e 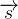 originem
originem  na mesma direção, e
na mesma direção, e
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=-\int _{C}\overrightarrow {F}\cdot d\overrightarrow {s} \]](images/img-0721.png) |
se 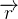 e
e 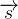 originam
originam  em direções opostas. O que fizemos para o plano, vale também para o espaço, ou seja, se
em direções opostas. O que fizemos para o plano, vale também para o espaço, ou seja, se
![\[ \overrightarrow {F}=M\mathbf{i}+N\mathbf{j}+P\mathbf{k} \]](images/img-0722.png) |
com 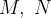 e
e 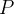 funções escalares e suponha que
funções escalares e suponha que  parametrizada por
parametrizada por
![\[ x=f(t),\ y=g(t),\ z=h(t),\ \ a\leq t\leq b \]](images/img-0723.png) |
assim
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{C}Mdx+Ndy+Pdz \]](images/img-0724.png) |
ou
![\[ =\int _{a}^{b}M(f(t),g(t),h(t))f^{\prime }(t)dt+\int _{a}^{b}N(f(t),g(t),h(t))g^{\prime }(t)dt+\int _{a}^{b}P(f(t),g(t),h(t))h^{\prime }(t)dt. \]](images/img-0725.png) |
Seja 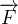 um campo vetorial
um campo vetorial
![\[ \overrightarrow {F}(x,y)=\sqrt{y}\mathbf{i}+\left( x^{3}+y\right) \mathbf{j} \]](images/img-0726.png) |
calcular a integral de linha de 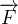 desde
desde 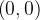 a
a 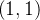 ao longo das curvas
ao longo das curvas
a) a reta 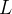 de equações paramétricas
de equações paramétricas 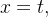
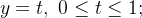
b) o caminho  de equações paramétricas
de equações paramétricas 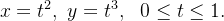
Para o caminho de parte (a)  seja
seja 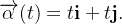 Então
Então 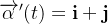 e
e 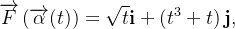 assim,
assim,
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {\alpha }=\int _{(0,0)}^{(1,1)}\overrightarrow {F}\cdot d\overrightarrow {\alpha }=\int _{0}^{1}\left( \sqrt{t}+t^{3}+t\right) dt=\left( \frac{2}{3}t^{\frac{3}{2}}+\frac{t^{4}}{4}+\frac{t^{2}}{2}\right) |_{0}^{1}=\frac{17}{12} \]](images/img-0735.png) |
(b) Tomamos  então
então 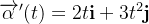 e
e
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {\alpha }=\int _{0}^{1}\overrightarrow {F}(\overrightarrow {\alpha }(t))\cdot d\overrightarrow {\alpha }^{\prime }(t)=\int _{0}^{1}\left( 2t^{\frac{5}{2}}+3t^{8}+3t^{5}\right) dt=\frac{59}{42}. \]](images/img-0738.png) |
Eis um exemplo em a integral depende do caminho em que se está integrando.