| Cálculo Diferencial e Integral 3 |
Um campo vetorial em três dimensões é uma função 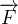 cujo domínio
cujo domínio 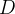 é um subconjunto do
é um subconjunto do 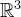 e cujo contradomínio é um subconjunto do
e cujo contradomínio é um subconjunto do 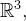 ou seja,
ou seja,
 |
![$\displaystyle \begin{array}[c]{cc}\overrightarrow {F}: & \ \ \mathbb {R}^{3}\rightarrow \mathbb {R}^{3}\end{array} $](images/img-0623.png) |
|||
 |
![$\displaystyle \begin{array}[c]{cc}& (x,y)\rightarrow F(x,y,z) \end{array} $](images/img-0624.png) |
onde
![\[ \overrightarrow {F}(x,y,z)=M(x,y,z)\mathbf{i}+N(x,y,z)\mathbf{j}+P(x,y,z)\mathbf{k} \]](images/img-0625.png) |
e 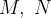 e
e 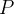 são funções escalares.
são funções escalares.
Em duas dimensões
![\[ \overrightarrow {F}(x,y)=M(x,y)\mathbf{i}+N(x,y)\mathbf{j} \]](images/img-0627.png) |
Seja 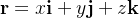 o vetor posição de
o vetor posição de  e denotemos por
e denotemos por 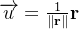 o vetor unitário com a mesma direção de
o vetor unitário com a mesma direção de  Um campo vetorial
Um campo vetorial 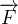 é um campo quadrado inverso se
é um campo quadrado inverso se
![\[ \overrightarrow {F}(x,y,z)=\frac{c}{\left\Vert \mathbf{r}\right\Vert ^{2}}\overrightarrow {u}=\frac{c}{\left\Vert \mathbf{r}\right\Vert ^{3}}\mathbf{r} \]](images/img-0631.png) |
Note que
![\[ \overrightarrow {F}(x,y,z)=\frac{c}{\left\Vert \mathbf{r}\right\Vert ^{3}}\mathbf{r=}\frac{c}{\left( x^{2}+y^{2}+z^{2}\right) ^{3/2}}\left( x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\right) \]](images/img-0632.png) |
Exemplos: Força de gravidade. Lei de gravitação universal de Newton
![\[ \overrightarrow {F}(x,y,z)=-G\frac{m_{0}m}{\left\Vert \mathbf{r}\right\Vert ^{2}}\overrightarrow {u}. \]](images/img-0633.png) |
Lei de Coulomb
![\[ \overrightarrow {F}(x,y,z)=-c\frac{Qq}{\left\Vert \mathbf{r}\right\Vert ^{2}}\overrightarrow {u}. \]](images/img-0634.png) |
Se  é uma função escalar então
é uma função escalar então 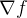 é um campo vetorial definido por
é um campo vetorial definido por
![\[ \nabla f=\frac{\partial f}{\partial x}\mathbf{i}+\frac{\partial f}{\partial y}\mathbf{j}+\frac{\partial f}{\partial z}\mathbf{k.} \]](images/img-0636.png) |
Um campo vetorial 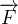 é conservativo se
é conservativo se
![\[ \overrightarrow {F}(x,y,z)=\nabla f(x,y,z) \]](images/img-0637.png) |
para alguma função escalar 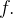
Se 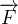 é conservativo, então a função
é conservativo, então a função  é a função potencial para
é a função potencial para 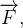
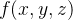 é o potencial no ponto
é o potencial no ponto 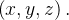
Se  está no domínio de
está no domínio de  então o vetor gradiente
então o vetor gradiente 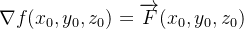 é normal à superfície de nível
é normal à superfície de nível  de
de  que contém o ponto
que contém o ponto 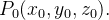
A superfície  é o gráfico de
é o gráfico de 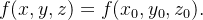
Todo vetor 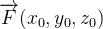 num campo vetorial conservativo é normal à superfície de nível de uma função potencial
num campo vetorial conservativo é normal à superfície de nível de uma função potencial  para
para 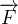 que contém
que contém 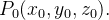
Todo campo vetorial quadrado inverso é conservativo.
Prova: Seja 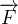 um campo quadrado inverso, isto é,
um campo quadrado inverso, isto é,
![\[ \overrightarrow {F}(x,y,z)=\frac{cx}{\left( x^{2}+y^{2}+z^{2}\right) ^{3/2}}\mathbf{i}+\frac{cy}{\left( x^{2}+y^{2}+z^{2}\right) ^{3/2}}\mathbf{j}+\frac{cz}{\left( x^{2}+y^{2}+z^{2}\right) ^{3/2}}\mathbf{k} \]](images/img-0648.png) |
se considerarmos
![\[ f(x,y,z)=\frac{-c}{\left( x^{2}+y^{2}+z^{2}\right) ^{1/2}}=-\dfrac {c}{r},\ \ \text {onde }r=\left\Vert \mathbf{r}\right\Vert =\left( x^{2}+y^{2}+z^{2}\right) ^{1/2} \]](images/img-0649.png) |
então
![\[ \nabla f(x,y,z)=\overrightarrow {F}(x,y,z). \]](images/img-0650.png) |
As superficies de nível para  são os gráficos da equação
são os gráficos da equação
![\[ -\frac{c}{\left( x^{2}+y^{2}+z^{2}\right) ^{1/2}}=k,\ \ \ \left( k<0\right) \]](images/img-0651.png) |
Assim
![\[ x^{2}+y^{2}+z^{2}=\frac{c^{2}}{k^{2}}. \]](images/img-0652.png) |
As superfícies são esferas com centro na origem.
Se  onde
onde  e
e 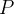 tem derivadas parciais em alguma região. O rotacional de
tem derivadas parciais em alguma região. O rotacional de 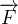 é dado por
é dado por
![\[ rot\ \overrightarrow {F}=\nabla \times \overrightarrow {F}=\left( \frac{\partial P}{\partial y}-\frac{\partial N}{\partial z}\right) \mathbf{i}+\left( \frac{\partial M}{\partial z}-\frac{\partial P}{\partial x}\right) \mathbf{j}+\left( \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) \mathbf{k.} \]](images/img-0655.png) |
Notação:
![\[ rot\ \overrightarrow {F}=\nabla \times \overrightarrow {F}=\left\vert \begin{array}[c]{ccc}i & j & k\\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ M & N & P \end{array} \right\vert \]](images/img-0656.png) |
Seja 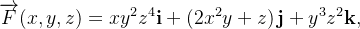 ache
ache 
Solução: ![$\nabla \times \overrightarrow {F}=\left\vert \begin{array}[c]{ccc}i & j & k\\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ xy^{2}z^{4} & 2x^{2}y+z & y^{3}z^{2}\end{array} \right\vert =\left( 3y^{2}z^{2}-1\right) \mathbf{i}+4xy^{2}z^{3}\mathbf{j}+\left( 4xy-2xyz^{4}\right) \mathbf{k.}$](images/img-0659.png)
Seja 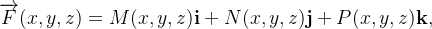 com
com  e
e 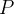 com derivadas parciais em alguma região. A divergência de
com derivadas parciais em alguma região. A divergência de 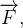 é dada por
é dada por
![\[ \operatorname {div}F=\nabla \cdot \overrightarrow {F}=\frac{\partial M}{\partial x}+\frac{\partial N}{\partial y}+\frac{\partial P}{\partial z}. \]](images/img-0661.png) |
Se  ache o
ache o 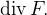
Solução:
![\[ \operatorname {div}F=y^{2}z^{4}+2x^{2}+2y^{3}z. \]](images/img-0664.png) |