10.2 Aplicação

Considere 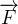$\overrightarrow {F}$ um campo de forças: 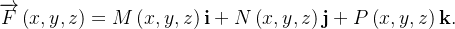$\overrightarrow {F}\left( x,y,z\right) =M\left( x,y,z\right) \mathbf{i}+N\left( x,y,z\right) \mathbf{j}+P\left( x,y,z\right) \mathbf{k.}$ Queremos calcular o trabalho realizado pelo campo de forças ao longo de uma curva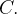 $C.$

$C$ parametrizada por:

$x=g(t),\ y=h(t),\ z=k(t),\ a\leq t\leq b.$

Considere uma partição de $\left[ a,b\right]$

$P=\left\{ a=t_{0}<t_{1}<\cdots <t_{n}=b\right\} .$

Para o ponto 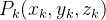$P_{k}(x_{k},y_{k},z_{k})$ há um valor 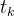$t_{k}$ associado. Denotamos

$\Delta x_{k}=x_{k}-x_{k-1},\ \ \Delta y_{k}=y_{k}-y_{k-1},\ \ \Delta z_{k}=z_{k}-z_{k-1}.$

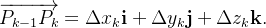$\overrightarrow {P_{k-1}P_{k}}=\Delta x_{k}\mathbf{i}+\Delta y_{k}\mathbf{j}+\Delta z_{k}\mathbf{k.}$ Tomemos a soma de Riemann

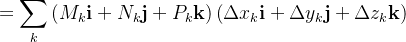	$\displaystyle \sum _{k}\overrightarrow {F}_{k}\cdot \overrightarrow {P_{k-1}P_{k}}$	$\displaystyle =\sum _{k}\left( M_{k}\mathbf{i}+N_{k}\mathbf{j}+P_{k}\mathbf{k}\right) \left( \Delta x_{k}\mathbf{i}+\Delta y_{k}\mathbf{j}+\Delta z_{k}\mathbf{k}\right)$
	$\displaystyle$	$\displaystyle =\sum _{k}\left( M_{k}\Delta x_{k}+N_{k}\Delta y_{k}+P_{k}\Delta z_{k}\right)$

daí

$\lim _{\left\vert p\right\vert \rightarrow 0}\sum _{k}\left( M_{k}\Delta x_{k}+N_{k}\Delta y_{k}+P_{k}\Delta z_{k}\right) =\int _{C}Mdx+Ndy+Pdz.$

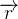Se $s$ é parâmetro de comprimento de arco da curva $C$ e $\overrightarrow {r}$ é o vetor posição do ponto na curva

$\overrightarrow {r}(s)=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$

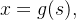
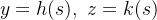onde $x=g(s),$ $y=h(s),\ z=k(s)$ então o vetor tangente a curva $C$ em cada ponto é

$\overrightarrow {T}(s)=\frac{d\overrightarrow {r}}{ds}=\frac{dx}{ds}\mathbf{i}+\frac{dy}{ds}\mathbf{j}+\frac{dz}{ds}\mathbf{k}$

A componente tangencial da força 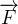$\overrightarrow {F}$ em cada ponto é:

$\overrightarrow {F}\cdot \overrightarrow {T}(s)=M\frac{dx}{ds}+N\frac{dy}{ds}+P\frac{dz}{ds}.$

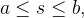Logo, se $a\leq s\leq b,$ temos que

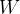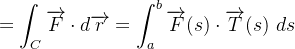	$\displaystyle W$	$\displaystyle =\int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{a}^{b}\overrightarrow {F}(s)\cdot \overrightarrow {T}(s)\ ds$
	$\displaystyle$	$\displaystyle =\int _{C}\left( M\frac{dx}{ds}+N\frac{dy}{ds}+P\frac{dz}{ds}\right) ds$

Se 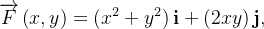$\overrightarrow {F}\left( x,y\right) =\left( x^{2}+y^{2}\right) \mathbf{i}+\left( 2xy\right) \mathbf{j,}$ calcular 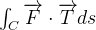$\int _{C}\overrightarrow {F}\cdot \overrightarrow {T}ds$ sobre as seguintes curvas

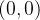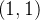(a) de $(0,0)$ a $\left( 1,1\right)$ sobre a reta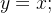 $y=x;$

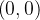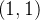(b) de $\left( 0,0\right)$ a $\left( 1,1\right)$ sobre a curva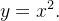 $y=x^{2}.$

(a) Podemos parametrizar a reta 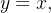$y=x,$ por

$x=t,\ y=t,\ 0\leq t\leq 1.$

Assim

	$\displaystyle \int _{C}\overrightarrow {F}\cdot \overrightarrow {T}ds$	$\displaystyle =\int _{C}\left( x^{2}+y^{2}\right) dx+\left( 2xy\right) dy$
	$\displaystyle$	$\displaystyle =\int _{0}^{1}[\left( t^{2}+t^{2}\right) +\left( 2t^{2}\right) ]dt$
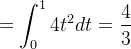	$\displaystyle$	$\displaystyle =\int _{0}^{1}4t^{2}dt=\frac{4}{3}$

Analogamente, para o caso (b) temos se a parábola for parametrizada por

$x=t,\ y=t^{2},\ 0\leq t\leq 1$

assim

$\int _{C}\overrightarrow {F}\cdot \overrightarrow {T}ds=\int _{0}^{1}\left[ \left( t^{2}+t^{4}\right) +\left( 2tt^{2}\right) 2t\right] dt=\int _{0}^{1}\left( t^{2}+5t^{4}\right) dt=\frac{4}{3}.$

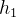A força gravitacional na vizinhança de um ponto da superfície da Terra é representada por $-mg\mathbf{j,}$ onde o eixo-y aponta para cima. Mostrar que o trabalho realizado por essa força sobre um corpo que se desloca, num plano vertical, da altura $h_{1}$ até a altura 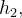$h_{2},$ seguindo qualquer caminho é igual a $mg(h_{1}-h_{2}).$

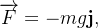Seja $\overrightarrow {F}=-mg\mathbf{j,}$ a força de gravidade que atua no corpo numa posição 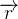$\overrightarrow {r}$ se esse 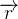$\overrightarrow {r}$ representa a curva em que o corpo está se deslocando podemos dizer que

$\overrightarrow {r}(t)=\alpha (t)\mathbf{i}+\beta (t)\mathbf{j}$

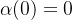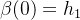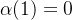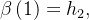onde $\alpha (0)=0$ e $\beta (0)=h_{1}$ e $\alpha (1)=0$ e $\beta \left( 1\right) =h_{2},$ o trabalho que atua no corpo será dado por

$W=\int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=-\int _{0}^{1}mg\beta ^{\prime }(t)dt=-mg\left( \beta (t)\right) |_{0}^{1}=-mg\left( h_{2}-h_{1}\right) =mg\left( h_{1}-h_{2}\right) .$

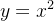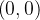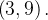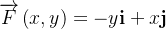Seja $C$ a parte da parábola $y=x^{2}$ entre os pontos $\left( 0,0\right)$ e $\left( 3,9\right) .$ Se $\overrightarrow {F}\left( x,y\right) =-y\mathbf{i}+x\mathbf{j}$ é uma força que atua em 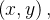$\left( x,y\right) ,$ ache o trabalho realizado por 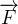$\overrightarrow {F}$ ao longo de $C$ de

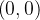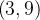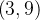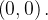
(a) $\left( 0,0\right)$ a $\left( 3,9\right) \ \ \ \ \ \ \ \$ (b) $\left( 3,9\right)$ a $\left( 0,0\right) .$

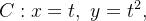
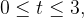$C:x=t,\ y=t^{2},$ $0\leq t\leq 3,$ obtemos

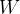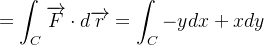	$\displaystyle W$	$\displaystyle =\int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{C}-ydx+xdy$
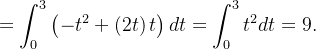	$\displaystyle$	$\displaystyle =\int _{0}^{3}\left( -t^{2}+\left( 2t\right) t\right) dt=\int _{0}^{3}t^{2}dt=9.$