10.1 Aplicação
Imagine uma curva  no espaço tridimensional como um fio de arame delgado com densidade variável. Suponha que a densidade é expressa por
no espaço tridimensional como um fio de arame delgado com densidade variável. Suponha que a densidade é expressa por 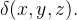 A massa total do arame é
A massa total do arame é
o centro de gravidade se define por
Um arame de densidade constante se chama uniforme. Neste caso, o centro de gravidade é o centróide.
Calcular a massa do arame 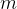 de uma mola que tem a forma de uma hélice cuja equação vetorial é
de uma mola que tem a forma de uma hélice cuja equação vetorial é
se a densidade em

é
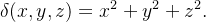
A integral para calcular 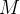 é
é
dai
Neste exemplo,
Assim
De modo análogo, se calcula

e
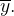
O momento de inércia de um arame delgado de densidade 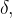 em relação a uma reta
em relação a uma reta 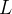 é definido por
é definido por
onde 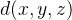 é a distância de um ponto
é a distância de um ponto  de
de  a
a 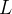 e
e 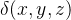 é a densidade do arame.
é a densidade do arame.
Calcular o momento de inércia 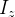 da mola do exemplo anterior.
da mola do exemplo anterior.
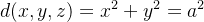 e
e 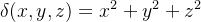 então
então
 no espaço tridimensional como um fio de arame delgado com densidade variável. Suponha que a densidade é expressa por
no espaço tridimensional como um fio de arame delgado com densidade variável. Suponha que a densidade é expressa por 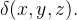 A massa total do arame é
A massa total do arame é ![\[ m=\int _{C}\delta (x,y,z)ds \]](images/img-0740.png)
![\[ \overline{x}m=\int _{C}x\delta (x,y,z)d,\ \ \overline{y}m=\int _{C}y\delta (x,y,z)ds,\ \ \overline{z}m=\int _{C}z\delta (x,y,z)ds. \]](images/img-0741.png)
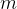 de uma mola que tem a forma de uma hélice cuja equação vetorial é
de uma mola que tem a forma de uma hélice cuja equação vetorial é ![\[ \overrightarrow {\alpha }(t)=a\cos t\mathbf{i}+a\operatorname {sen}t\mathbf{j}+bt\mathbf{k,\ \ }0\leq t\leq 2\pi , \]](images/img-0742.png)
 é
é 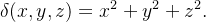
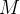 é
é 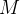
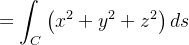

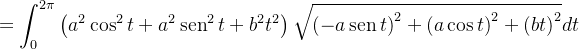
![\[ M=\sqrt{a^{2}+b^{2}}\int _{0}^{2\pi }\left( a^{2}+b^{2}t^{2}\right) dt=\sqrt{a^{2}+b^{2}}\left( 2\pi a^{2}+\frac{8}{3}\pi ^{3}b^{2}\right) . \]](images/img-0748.png)
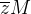
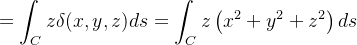


![\[ \overline{z}=\frac{2\pi a^{2}+\frac{8}{3}\pi ^{3}b^{2}}{b\left( 2\pi ^{2}a^{2}+4\pi ^{4}b^{2}\right) }. \]](images/img-0752.png)
 e
e 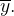
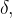 em relação a uma reta
em relação a uma reta 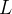 é definido por
é definido por![\[ I_{L}=\int _{C}d^{2}(x,y,z)\delta (x,y,z)ds, \]](images/img-0755.png)
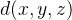 é a distância de um ponto
é a distância de um ponto  de
de  a
a 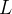 e
e 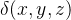 é a densidade do arame.
é a densidade do arame. 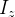 da mola do exemplo anterior.
da mola do exemplo anterior. 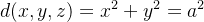 e
e 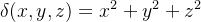 então
então![\[ I_{z}=\int _{C}\left( x^{2}+y^{2}\right) \left( x^{2}+y^{2}+z^{2}\right) ds=a^{2}\int _{C}\left( x^{2}+y^{2}+z^{2}\right) ds=a^{2}M. \]](images/img-0759.png)