| Cálculo Diferencial e Integral 3 |
Integrais que tem o mesmo valor ao longo de qualquer caminho que una dois pontos 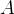 e
e 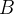 são integrais independentes do caminho.
são integrais independentes do caminho.
Se a integral  é independente do caminho então podemos denotá-la por
é independente do caminho então podemos denotá-la por  Analogamente vale para
Analogamente vale para 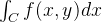 e
e 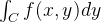 e integrais em três dimensões.
e integrais em três dimensões.
Região Conexa: Dois pontos quaisquer da região podem ser ligados por uma curva (parcialmente) suave, inteiramente contidas na região.
Se 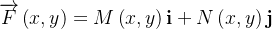 é contínua numa região conexa aberta
é contínua numa região conexa aberta 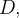 então a integral curvilínea
então a integral curvilínea 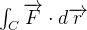 é independente do caminho se, e somente se,
é independente do caminho se, e somente se, 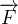 é conservativo. Isto é, existe uma função escalar
é conservativo. Isto é, existe uma função escalar  tal que
tal que 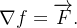
Suponha que exista  tal que
tal que 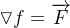
![\[ \overrightarrow {F}\left( x,y\right) =M\left( x,y\right) \mathbf{i}+N\left( x,y\right) \mathbf{j=}\frac{\partial f}{\partial x}\mathbf{i}+\frac{\partial f}{\partial y}\mathbf{j} \]](images/img-0824.png) |
sejam 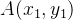 ,
, 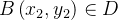 e
e  uma curva arbitrária ligando
uma curva arbitrária ligando 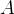 e
e 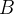 então
então
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{C}M\left( x,y\right) dx+N\left( x,y\right) dy=\int _{C}\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy \]](images/img-0827.png) |
se  admite a parametrização:
admite a parametrização: 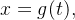
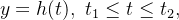 então
então
![\[ \int _{C}\overrightarrow {F}\cdot d\overrightarrow {r}=\int _{t_{1}}^{t_{2}}\left[ \frac{\partial f}{\partial x}\left( g(t),h(t)\right) g^{\prime }(t)+\frac{\partial f}{\partial y}\left( g(t),h(t)\right) h^{\prime }(t)\right] dt \]](images/img-0830.png) |
Pela regra da cadeia
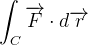 |
![$\displaystyle =\int _{t_{1}}^{t_{2}}\frac{d}{dt}\left[ f\left( g(t),h(t)\right) \right] dt $](images/img-0832.png) |
|||
 |
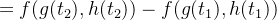 |
|||
 |
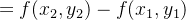 |
|||
 |
![$\displaystyle =\left[ f(x,y)\right] _{\left( x_{1},y_{1}\right) }^{\left( x_{2},y_{2}\right) }. $](images/img-0835.png) |
Em outras palavras: se 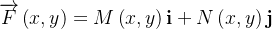
 é contínua em
é contínua em 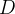 conexa aberta, e
conexa aberta, e  é uma curva parcialmente suave em
é uma curva parcialmente suave em 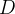 com extremidades
com extremidades 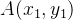 ,
, 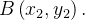 Se existe
Se existe  tal que
tal que 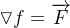 então
então
![\[ \int _{A(x_{1},y_{1})}^{B\left( x_{2},y_{2}\right) }\overrightarrow {F}\cdot d\overrightarrow {r}=\left[ f(x,y)\right] _{\left( x_{1},y_{1}\right) }^{\left( x_{2},y_{2}\right) }. \]](images/img-0837.png) |
Reciprocamente, suponha que a integral seja independente do caminho, defina
![\[ f(x,y)=\int _{(x_{0},y_{0})}^{(x,y)}\overrightarrow {F}\cdot d\overrightarrow {r} \]](images/img-0838.png) |
para todo 
 depende só de
depende só de  e
e  escolha um círculo
escolha um círculo  com centro
com centro 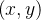 e seja
e seja 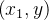 um ponto interior ao círculo
um ponto interior ao círculo 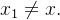 Temos que
Temos que
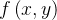 |
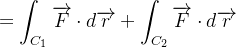 |
|||
 |
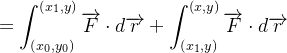 |
como a primeira integral não depende de 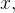 temos
temos
![\[ \frac{\partial f}{\partial x}\left( x,y\right) =\frac{\partial }{\partial x}\int _{\left( x_{1},y\right) }^{\left( x,y\right) }\overrightarrow {F}\cdot d\overrightarrow {r} \]](images/img-0848.png) |
seja 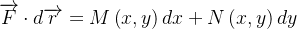 e
e 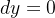 em
em 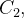 obtemos
obtemos
![\[ \frac{\partial f}{\partial x}\left( x,y\right) =\frac{\partial }{\partial x}\int _{\left( x_{1},y\right) }^{\left( x,y\right) }M\left( x,y\right) dx \]](images/img-0852.png) |
como 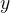 é fixo, então
é fixo, então 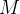 depende só de
depende só de 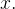 Assim
Assim
![\[ \frac{\partial f}{\partial x}\left( x,y\right) =M(x,y). \]](images/img-0853.png) |
De modo análogo, temos que
![\[ \frac{\partial f}{\partial y}\left( x,y\right) =N(x,y) \]](images/img-0854.png) |
ou seja,
![\[ \triangledown f=M\mathbf{i}+N\mathbf{j=}\overrightarrow {F}. \]](images/img-0855.png) |
A prova do teorema pode ser estendida a curvas parcialmente suaves subdividindo  num número finito de curvas suaves.
num número finito de curvas suaves.
A demonstração do teorema anterior nos dá um método para calcular integrais curvilíneas que não dependem do caminho. Descrevemos este método pelo seguinte teorema.
Seja 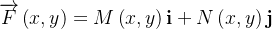
 contínua numa região aberta conexa
contínua numa região aberta conexa 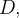 e
e  uma curva parcialmente suave em
uma curva parcialmente suave em 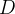 com extremidades
com extremidades 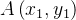 e
e 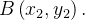 Se
Se  então
então
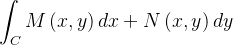 |
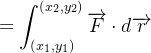 |
|||
 |
![$\displaystyle =\left[ f\left( x,y\right) \right] _{\left( x_{1},y_{1}\right) }^{\left( x_{2},y_{2}\right) }. $](images/img-0859.png) |
Se uma integral curvilínea 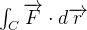 é independente do caminho, então, pelo Teorema anterior com
é independente do caminho, então, pelo Teorema anterior com 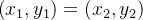 vemos que
vemos que 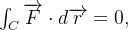 para toda curva fechada simples
para toda curva fechada simples 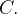
Seja 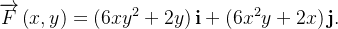
(a) Mostre que 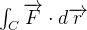
 é independente do caminho.
é independente do caminho.
(b) Calcule  .
.
(a) Pelo Teorema anterior a integral curvilínea é independente do caminho se, e somente se, existe uma função diferenciável  tal que
tal que
![\[ \nabla f\left( x,y\right) =\overrightarrow {F}\left( x,y\right) \]](images/img-0864.png) |
isto é,
![\[ \frac{\partial f}{\partial x}\mathbf{i}+\frac{\partial f}{\partial y}\mathbf{j=}\left( 6xy^{2}+2y\right) \mathbf{i}+\left( 6x^{2}y+2x\right) \mathbf{j} \]](images/img-0865.png) |
ou
![\[ \frac{\partial f}{\partial x}=6xy^{2}+2y\text { \ e \ }\frac{\partial f}{\partial y}=6x^{2}y+2x\text {\ \ } \]](images/img-0866.png) |
integrando (parcialmente) 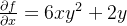
 em relação a
em relação a 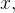 obtemos
obtemos
![\[ f(x,y)=3x^{2}y^{2}+2yx+h(y) \]](images/img-0869.png) |
onde 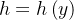 depende só de
depende só de  Diferenciando
Diferenciando  em relação a
em relação a 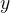 temos
temos
![\[ \frac{\partial f}{\partial y}=6x^{2}y+2x+h^{\prime }(y)=6x^{2}y+2x \]](images/img-0871.png) |
logo
![\[ h^{\prime }(y)=0 \]](images/img-0872.png) |
o que implica em
![\[ h\left( y\right) =c\ \text {\ }\left( c\text { constante}\right) \]](images/img-0873.png) |
segue que
![\[ f(x,y)=3x^{2}y^{2}+2yx+c \]](images/img-0874.png) |
e  é tal que
é tal que
![\[ \nabla f\left( x,y\right) =\overrightarrow {F}\left( x,y\right) . \]](images/img-0875.png) |
(b) Como qualquer função potencial serve para calcular a integral, aplicamos o Teorema anterior com 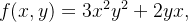 assim,
assim,
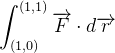 |
![$\displaystyle =\left[ f\left( x,y\right) \right] _{\left( 1,0\right) }^{\left( 1,1\right) }=\left[ 3x^{2}y^{2}+2yx\right] _{\left( 1,0\right) }^{\left( 1,1\right) } $](images/img-0878.png) |
|||
 |
![$\displaystyle =\left[ \left( 3.1^{2}.1^{2}+2.1.1\right) -\left( 3.1^{2}.0^{2}+2.0.1\right) \right] =5. $](images/img-0879.png) |
Se 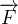 é um campo de forças conservativo em duas dimensões então o trabalho realizado por
é um campo de forças conservativo em duas dimensões então o trabalho realizado por 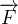 ao longo de qualquer caminho
ao longo de qualquer caminho  de
de 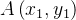 a
a  é igual à diferença de potenciais entre
é igual à diferença de potenciais entre 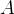 e
e 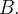
Seja
![\[ W=\int _{\left( x_{1},y_{1}\right) }^{\left( x_{2},y_{2}\right) }\overrightarrow {F}\cdot d\overrightarrow {r}=f\left( x_{2},y_{2}\right) -f\left( x_{1},y_{1}\right) . \]](images/img-0882.png) |
Se a integral independe do caminho e se tomamos  curva fechada e
curva fechada e 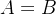 então a diferença de potencial é zero, e assim
então a diferença de potencial é zero, e assim
![\[ W=0. \]](images/img-0884.png) |
Reciprocamente, se 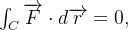 para toda curva fechada
para toda curva fechada  simples,
simples,  então a integral é independente do caminho e o campo é conservativo.
então a integral é independente do caminho e o campo é conservativo.
Seja 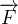 o campo gravitacional de uma partícula de massa
o campo gravitacional de uma partícula de massa 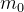 situada na origem de um sistema coordenado
situada na origem de um sistema coordenado 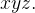 Ache o trabalho realizado por
Ache o trabalho realizado por 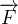 quando uma partícula de massa
quando uma partícula de massa 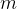 se move de
se move de 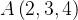 a
a 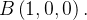
A força gravitacional das duas partícula é dada por
![\[ \overrightarrow {F}\left( x,y,z\right) =-G\frac{m_{0}m}{\left\Vert \overrightarrow {r}\right\Vert }\overrightarrow {r} \]](images/img-0889.png) |
onde 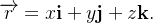 Temos que
Temos que
![\[ f\left( x,y,z\right) =\frac{Gm_{0}m}{\left( x^{2}+y^{2}+z^{2}\right) ^{1/2}} \]](images/img-0891.png) |
é o potencial de 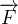 . Logo,
. Logo,
![\[ W=\int _{A}^{B}\overrightarrow {F}\cdot d\overrightarrow {r}=\left[ \frac{Gm_{0}m}{\left( x^{2}+y^{2}+z^{2}\right) ^{1/2}}\right] _{\left( 2,3,4\right) }^{\left( 1,0,0\right) }=Gm_{0}m\left( 1-\frac{1}{\sqrt{29}}\right) \]](images/img-0892.png) |
Se a integral  é independente do caminho, então, pelo teorema anterior, existe uma função
é independente do caminho, então, pelo teorema anterior, existe uma função  tal que
tal que
![\[ M=\frac{\partial f}{\partial x}\ \ \ \text {e \ \ }N=\frac{\partial f}{\partial y} \]](images/img-0894.png) |
Consequentemente 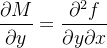 e
e  Se
Se  e
e  têm derivadas parciais primeiras contínuas, então
têm derivadas parciais primeiras contínuas, então  e
e
![\[ \frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}. \]](images/img-0899.png) |
A recíproca é falsa, a menos que se ponha restrições sobre o domínio  de
de 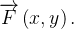 Em particular, se
Em particular, se 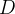 é uma região simplesmente conexa (não há buracos), então a condição
é uma região simplesmente conexa (não há buracos), então a condição 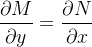 implica que a integral
implica que a integral  é independente do caminho.
é independente do caminho.
Se 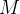 e
e 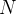 têm derivadas parciais primeiras contínuas numa região simplesmente conexa
têm derivadas parciais primeiras contínuas numa região simplesmente conexa 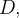 então a integral curvilínea
então a integral curvilínea
![\[ \int _{C}M\left( x,y\right) dx+N\left( x,y\right) dy \]](images/img-0902.png) |
é independente do caminho em 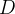 se, e somente se,
se, e somente se,
![\[ \frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}. \]](images/img-0899.png) |
Mostre que a integral curvilínea
![\[ \int _{C}\left( e^{3y}-y^{2}\operatorname {sen}x\right) dx+\left( 3xe^{3y}+2y\cos x\right) dy \]](images/img-0903.png) |
Sejam
![\[ M\left( x,y\right) =e^{3y}-y^{2}\operatorname {sen}x,\ \ N\left( x,y\right) =3xe^{3y}+2y\cos x \]](images/img-0904.png) |
![\[ \frac{\partial M}{\partial y}=3e^{3y}-2y\operatorname {sen}x,\ \ \frac{\partial N}{\partial x}=3e^{3y}-2y\operatorname {sen}x \]](images/img-0905.png) |
![\[ \frac{\partial M}{\partial y}=\frac{\partial N}{\partial x} \]](images/img-0906.png) |
Determine se a integral 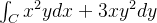 é independente do caminho.
é independente do caminho.
Sejam
![\[ M\left( x,y\right) =x^{2}y,\ \ \ N\left( x,y\right) =3xy^{2} \]](images/img-0908.png) |
![\[ \frac{\partial M}{\partial y}=x^{2},\ \ \frac{\partial N}{\partial x}=3y^{2} \]](images/img-0909.png) |
![\[ \frac{\partial M}{\partial y}\neq \frac{\partial N}{\partial x} \]](images/img-0910.png) |
Seja 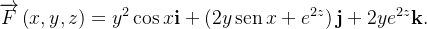
(a) Mostre que 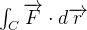 é independente do caminho, e ache uma função potencial
é independente do caminho, e ache uma função potencial  para
para 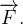
(b) Se 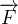 é um campo de forças, ache o trabalho realizado por
é um campo de forças, ache o trabalho realizado por 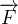 ao longo de qualquer curva
ao longo de qualquer curva  de
de 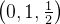 a
a 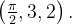
(a) A integral será independente do caminho se existir uma função diferenciável 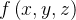 tal que
tal que 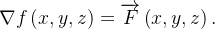 Ou seja,
Ou seja,
![\[ \frac{\partial f}{\partial x}=y^{2}\cos x, \]](images/img-0917.png) |
![\[ \frac{\partial f}{\partial y}=2y\operatorname {sen}x+e^{2z}, \]](images/img-0918.png) |
![\[ \frac{\partial f}{\partial z}=2ye^{2z}. \]](images/img-0919.png) |
Integrando 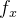 em relação a
em relação a 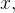 obtemos
obtemos
![\[ f(x,y,z)=y^{2}\operatorname {sen}x+g(y,z) \]](images/img-0921.png) |
diferenciando  em relação a
em relação a 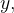 temos
temos
![\[ f_{y}=2y\operatorname {sen}x+g_{y}\left( y,z\right) =2y\operatorname {sen}x+e^{2z} \]](images/img-0922.png) |
daí
![\[ g_{y}\left( y,z\right) =e^{2z} \]](images/img-0923.png) |
integrando 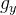 em relação a
em relação a 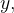 obtemos
obtemos
![\[ g\left( y,z\right) =ye^{2z}+k(z) \]](images/img-0925.png) |
substituindo esse valor em 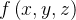 temos
temos
![\[ f\left( x,y,z\right) =y^{2}\operatorname {sen}x+ye^{2z}+k\left( z\right) \]](images/img-0926.png) |
diferenciando essa última função em relação a 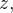 temos
temos
![\[ f_{z}=2ye^{2z}+k^{\prime }(z)=2ye^{2z} \]](images/img-0927.png) |
segue que
![\[ k^{\prime }(z)=0 \]](images/img-0928.png) |
o que implica
![\[ k(z)=c \]](images/img-0929.png) |
segue que
![\[ f(x,y,z)=y^{2}\operatorname {sen}x+ye^{2z}+c. \]](images/img-0930.png) |
(b) aplicando o teorema anterior, temos
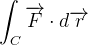 |
![$\displaystyle =\left[ y^{2}\operatorname {sen}x+ye^{2z}\right] _{\left( 0,1,\frac{1}{2}\right) }^{\left( \frac{\pi }{2},3,2\right) } $](images/img-0931.png) |
|||
 |
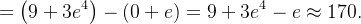 |
Seja 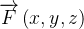 um campo vetorial de forças conservativo com função potencial
um campo vetorial de forças conservativo com função potencial 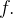 A energia potencial
A energia potencial  de uma partícula no ponto
de uma partícula no ponto  é
é
![\[ p\left( x,y,z\right) =-f\left( x,y,z\right) . \]](images/img-0935.png) |
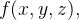
![\[ \overrightarrow {F}\left( x,y,z\right) =-\nabla p\left( x,y,z\right) \]](images/img-0937.png) |
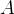 e
e 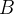 são dois pontos, então,
são dois pontos, então, ![\[ W=\int _{A}^{B}\overrightarrow {F}.d\overrightarrow {r}=\left[ -p\left( x,y,z\right) \right] _{A}^{b}=p\left( A\right) -p\left( B\right) \]](images/img-0938.png) |
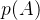 e
e 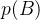 denotam a energia potencial em
denotam a energia potencial em 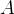 e
e 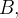 respectivamente.
respectivamente. A energia cinética é definida por 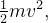
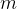 é a massa, e
é a massa, e 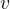 é a velocidade.
é a velocidade.
Lei de Conservação da Energia:
Se uma partícula se move de um ponto a outro num campo vetorial de forças conservativo, então a soma das energias cinética e potencial permanece constante.
Seja 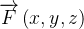 um campo conservativo de forças, temos
um campo conservativo de forças, temos
![\[ C:x=g(t),\ \ y=h(t),\ \ z=k(t),\ a\leq t\leq b; \]](images/img-0943.png) |
temos que
![\[ \overrightarrow {r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k~ \ }\text {(vetor posição)} \]](images/img-0944.png) |
![\[ \overrightarrow {v}=\frac{d\overrightarrow {r}}{dt}=\frac{dx}{dt}i+\frac{dy}{dt}\mathbf{j}+\frac{dz}{dt}\mathbf{k\ \ }\text {(vetor velocidade)}\mathbf{~ } \]](images/img-0945.png) |
![\[ \overrightarrow {a}=\frac{d\overrightarrow {v}}{dt}\ \ \text {(aceleração)} \]](images/img-0946.png) |
o trabalho é:
![\[ W=\int _{A}^{B}\overrightarrow {F}.d\overrightarrow {r}=\int _{a}^{b}\left( \overrightarrow {F}.\frac{d\overrightarrow {r}}{dt}\right) dt=\int _{a}^{b}\left( \overrightarrow {F}.\overrightarrow {v}\right) dt \]](images/img-0947.png) |
pela 2 lei de Newton
lei de Newton
![\[ \overrightarrow {F}=m.\overrightarrow {a}=m.\frac{d\overrightarrow {v}}{dt} \]](images/img-0949.png) |
e então
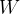 |
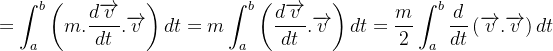 |
|||
 |
![$\displaystyle =\frac{m}{2}\int _{a}^{b}\frac{d}{dt}\left\vert \overrightarrow {v}\right\vert ^{2}dt=\frac{m}{2}\left[ v^{2}\right] _{a}^{b}=\frac{m}{2}\left( v^{2}\left( b\right) -v^{2}\left( a\right) \right) $](images/img-0951.png) |
segue que
![\[ W=K(B)-K(A) \]](images/img-0952.png) |
onde  é a energia cinética. Vimos que
é a energia cinética. Vimos que
![\[ W=p(A)-P(B). \]](images/img-0954.png) |
Assim
![\[ p(A)-P(B)=K(B)-K(A) \]](images/img-0955.png) |
o que implica
![\[ p(A)+K(A)=p(B)+K(B). \]](images/img-0956.png) |
o que prova a conservação da energia.