| Séries e Equações Diferenciais Ordinárias |
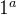 ordem
ordem Uma equação diferencial ordinária de 1 ordem é uma equação do tipo
ordem é uma equação do tipo
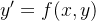 |
(5.1) |
onde 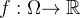 , é uma função dada e
, é uma função dada e 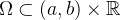 é um conjunto aberto;
é um conjunto aberto;  é uma variável independente, pertencente ao intervalo
é uma variável independente, pertencente ao intervalo 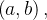 com
com 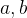 números reais
números reais 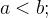 e
e 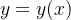 é a variável que depende de
é a variável que depende de  . Qualquer função
. Qualquer função 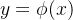 que satisfaça a edo (5.1) é dita solução dessa equação. Isto é, se
que satisfaça a edo (5.1) é dita solução dessa equação. Isto é, se 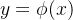 é solução então ela satisfaz
é solução então ela satisfaz
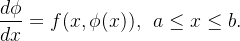 |
(5.2) |
Podemos impor uma condição inicial para essa equação, qual seja,
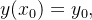 |
(5.3) |
quando consideramos a equação diferencial (5.1) junto com a condição inicial (5.3) então dizemos que se trata um problema de Cauchy. Condições são colocadas sobre a função  de modo que o problema de Cauchy
de modo que o problema de Cauchy
![\begin{equation} \left\{ \begin{array}[c]{c}y^{\prime }=f(x,y),\ \ x\in (a,b)\\ y(x_{0})=y_{0},\ x_{0}\in (a,b),\ y_{0}\in \mathbb {R}\end{array} \right.\label{probcauchy} \end{equation}](images/img-0940.png) |
(5.4) |
tenha uma única solução. À priori, a nossa função  pode ser qualquer função de duas variáveis. Mas para se garantir existência de soluções da equação diferencial (5.1)
pode ser qualquer função de duas variáveis. Mas para se garantir existência de soluções da equação diferencial (5.1)  teria de ser no mínimo contínua. Há dois teoremas importantes sobre existência de soluções que enunciamos a seguir.
teria de ser no mínimo contínua. Há dois teoremas importantes sobre existência de soluções que enunciamos a seguir.
Theorem 106 (Picard). Se  de
de 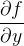 forem contínuas num domínio retangular
forem contínuas num domínio retangular  então há um intervalo
então há um intervalo  no qual existe uma única solução
no qual existe uma única solução 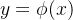 satisfazendo a equação diferencial (5.1) e as condições iniciais (5.3).
satisfazendo a equação diferencial (5.1) e as condições iniciais (5.3).
Theorem 107 (Peano). Se  é contínua num domínio retangular
é contínua num domínio retangular  então há um intervalo
então há um intervalo  no qual existe pelo menos uma solução
no qual existe pelo menos uma solução 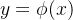 satisfazendo a equação diferencial (5.1) e as condições iniciais (5.3). Mas nesse caso, não se garante unicidade.
satisfazendo a equação diferencial (5.1) e as condições iniciais (5.3). Mas nesse caso, não se garante unicidade.
Por exemplo, dada a equação diferencial ordinária
![\[ y^{\prime } =xy^{1/2}, \quad y(0)=0 \]](images/img-0944.png) |
então 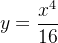 é solução dessa equação, pois,
é solução dessa equação, pois, 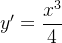 e
e 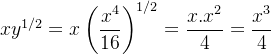 . Note que essa solução não é única, já que
. Note que essa solução não é única, já que 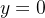 é também uma solução da equação diferencial junto com as condições iniciais.
é também uma solução da equação diferencial junto com as condições iniciais.
Example 108. A relação 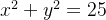 é uma solução implícita da equação diferencial
é uma solução implícita da equação diferencial
no intervalo
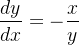
(5.5)
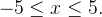
De fato, por diferenciação implícita, temos
![\[ \dfrac {d}{dx}[x^2+y^2]=\dfrac {d}{dx}(25) \]](images/img-0952.png) |
ou
![\[ 2x+2y y^{\prime }=0 \Rightarrow y^{\prime }=-\dfrac {x}{y}. \]](images/img-0953.png) |
Além disso, resolvendo 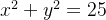 para
para 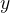 em termos de
em termos de  obtemos
obtemos 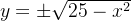 as duas funções
as duas funções 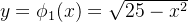 e
e 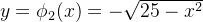 são soluções explícitas da edo (5.5) no intervalo
são soluções explícitas da edo (5.5) no intervalo 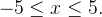
No caso mais simples em que a função  é linear em relação a variável
é linear em relação a variável 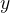 a nossa equação diferencial de 1
a nossa equação diferencial de 1 ordem se apresenta na forma
ordem se apresenta na forma
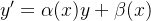 |
(5.6) |
onde 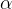 e
e 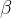 são funções reais quaisquer definidas no intervalo
são funções reais quaisquer definidas no intervalo 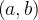 . Se supomos que
. Se supomos que 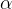 e
e 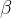 são funções cont
são funções cont nuas em
nuas em 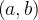 então esta equação tem uma resolução bem simples, pois se consideramos primeiro a equação linear homogênea associada à equação (5.6), isto é,
então esta equação tem uma resolução bem simples, pois se consideramos primeiro a equação linear homogênea associada à equação (5.6), isto é,
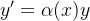 |
(5.7) |
podemos escrever tal equação na forma
![\[ \frac{y^{\prime }}{y}=\alpha (x) \]](images/img-0961.png) |
integrando em  temos
temos
![\[ \ln y=\int ^{x}\alpha (s)ds+c_{1}, \]](images/img-0962.png) |
onde 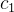 é uma constante arbitrária, segue que
é uma constante arbitrária, segue que
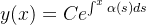 |
(5.8) |
é uma solução da equação homogênea (5.7) com 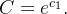 Usando agora o método de variação dos parâmetros para
Usando agora o método de variação dos parâmetros para 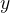 dada em (5.8) temos
dada em (5.8) temos
![\[ y^{\prime }=C^{\prime }e^{\int ^{x}\alpha (s)ds}+C\alpha (x)e^{\int ^{x}\alpha (s)ds} \]](images/img-0966.png) |
substituindo tal resultado em (5.6) obtemos
![\[ C^{\prime }e^{\int ^{x}\alpha (s)ds}+C\alpha (x)e^{\int ^{x}\alpha (s)ds}=C\alpha (x)e^{\int ^{x}\alpha (s)ds}+\beta (x) \]](images/img-0967.png) |
segue que
![\[ C^{\prime }e^{\int ^{x}\alpha (s)ds}=\beta (x) \]](images/img-0968.png) |
o que nos dá
![\[ C^{\prime }=\beta (x)e^{-\int ^{x}\alpha (s)ds} \]](images/img-0969.png) |
da
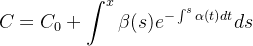 |
(5.9) |
onde 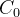 é uma constante arbitrária. Logo,
é uma constante arbitrária. Logo, 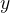 dada por
dada por
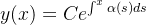 |
(5.10) |
onde  é definida em (5.9) é a solução geral de (5.6).
é definida em (5.9) é a solução geral de (5.6).
Vejamos alguns modelos matemáticos de algumas edos que podem ser físicos, biológicos, químicos, etc.
Crescimento Populacional
Modelo de Malthus
Se 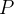 representa a população numa certa região num determinado instante
representa a população numa certa região num determinado instante 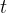 então
então
![\[ \dfrac {dP}{dt}=kP \, \, ( k \, \, \mbox{constante de proporcionalidade}) \]](images/img-0975.png) |
Modelo de Verhulst
![\[ \dfrac {dP}{dt}=(r-aP)P \]](images/img-0976.png) |
onde  e
e 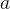 são constantes.
são constantes.
Decaimento Radioativo
A taxa 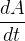 a qual o núcleo de uma substância decai é proporcional à quantidade
a qual o núcleo de uma substância decai é proporcional à quantidade 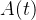 da substância remanescente no instante
da substância remanescente no instante 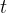
![\[ \dfrac {dA}{dt}=kA \, \, (k<0) \]](images/img-0979.png) |
Remark 109. Uma única equação diferencial pode servir como modelo matemático para vários fenômenos diferentes. Modelos matemáticos são frequentemente acompanhados por determinadas condições laterais. Por exemplo para o modelo de crescimento populacional esperaríamos conhecer a população inicial 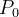 e no modelo de decaimento radiativo a quantidade inicial da substância radioativa.
e no modelo de decaimento radiativo a quantidade inicial da substância radioativa.
Lei de Resfriamento de Newton
De acordo com a Lei empírica de Newton do resfriamento, a taxa segundo a qual a temperatura de um corpo varia é proporcional à diferença entre a temperatura do corpo e a temperatura do meio que o rodeia, denominada de temperatura ambiente. Nesse caso, se 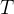 é a temperatura do corpo e
é a temperatura do corpo e 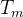 é temperatura do meio ambiente então
é temperatura do meio ambiente então
![\[ \dfrac {dT}{dt}=k(T-T_ m) \, \, (k<0). \]](images/img-0982.png) |
Disseminação de uma doença
Uma doença contagiosa espalha-se numa comunidade através do contato entre as pessoas. Seja 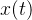 o número de pessoas que contraíram a doença e
o número de pessoas que contraíram a doença e 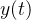 o número de pessoas que ainda não foram expostas. É razoável supor que a taxa
o número de pessoas que ainda não foram expostas. É razoável supor que a taxa 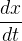 segundo a qual a doença se espalha seja proporcional ao número de encontros ou interações entre esses dois grupos de pessoas. Se supormos que o número de interações é proporcional ao produto
segundo a qual a doença se espalha seja proporcional ao número de encontros ou interações entre esses dois grupos de pessoas. Se supormos que o número de interações é proporcional ao produto 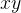 então
então
![\[ \dfrac {dx}{dt}=kxy \]](images/img-0987.png) |
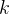 é a constante de proporcionalidade. Se a comunidade tem uma população fixa de
é a constante de proporcionalidade. Se a comunidade tem uma população fixa de 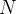 pessoas. O número de
pessoas. O número de 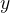 é
é 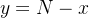 . Assim
. Assim
![\[ \dfrac {dx}{dt}=kx(N-x) \]](images/img-0990.png) |
se no instante inicial haviam 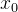 pessoas infectadas então
pessoas infectadas então 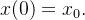
Misturas
No instante 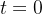 , um tanque contém
, um tanque contém 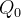 kg de sal dissolvido em
kg de sal dissolvido em 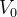 litros de água. Uma solução de sal em água com
litros de água. Uma solução de sal em água com 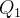 kg de sal por litro entra no tanque a uma razão de
kg de sal por litro entra no tanque a uma razão de 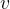 litros por minuto e a solução do tanque, bem misturada, sai a mesma razão. Seja
litros por minuto e a solução do tanque, bem misturada, sai a mesma razão. Seja 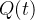 a quantidade de sal no tanque num instante
a quantidade de sal no tanque num instante 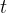 . A taxa de variação da quantidade de sal no tanque, no instante
. A taxa de variação da quantidade de sal no tanque, no instante 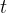 ,
, 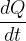 , é igual à taxa na qual o sal entra no tanque, menos a taxa na qual o sal sai do tanque. Logo,
, é igual à taxa na qual o sal entra no tanque, menos a taxa na qual o sal sai do tanque. Logo,
![\[ \dfrac {dQ}{dt}=vQ_1-\dfrac {v}{v_0}Q(t). \]](images/img-0999.png) |
Mecânica
A lei do movimento de Newton diz que
![\[ F=ma \]](images/img-1000.png) |
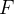 é a força externa,
é a força externa, 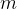 é massa,
é massa, 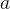 é a aceleração. Para um corpo que cai livremente num vácuo, e bastante próximo da terra, temos que
é a aceleração. Para um corpo que cai livremente num vácuo, e bastante próximo da terra, temos que
![\[ w=mg \]](images/img-1002.png) |
onde 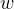 é o peso do corpo,
é o peso do corpo, 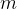 é massa do corpo e
é massa do corpo e 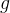 é a aceleração da gravidade. Mesmo que a massa do corpo permaneça constante, seu peso, e a aceleração da gravidade, alteram-se com a distância ao centro do campo gravitacional da terra. Para um corpo muito distante da terra
é a aceleração da gravidade. Mesmo que a massa do corpo permaneça constante, seu peso, e a aceleração da gravidade, alteram-se com a distância ao centro do campo gravitacional da terra. Para um corpo muito distante da terra
![\[ w=\dfrac {k}{(R+x)^2}, \]](images/img-1004.png) |
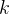 constante. Em
constante. Em 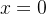 , temos que
, temos que 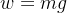 então
então 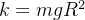 e, portanto,
e, portanto,
![\[ w=\dfrac {mgR^2}{(R+x)^2}. \]](images/img-1007.png) |