| Séries e Equações Diferenciais Ordinárias |
Dada uma função 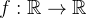 periódica de per
periódica de per odo
odo 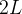 , integrável e absolutamente integrável, que possa ser escrita na forma:
, integrável e absolutamente integrável, que possa ser escrita na forma:
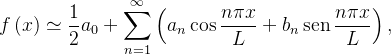 |
(4.14) |
a expressão do lado direito é a série de Fourier de  .
.
Que relação há entre  e sua série de Fourier? Será que a igualdade sempre ocorre?
e sua série de Fourier? Será que a igualdade sempre ocorre?
Vamos estudar as condições suficientes para que a função  seja igual à sua série de Fourier.
seja igual à sua série de Fourier.
Definition 90. Uma função 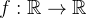 será seccionalmente cont
será seccionalmente cont nua se ela tiver apenas um número finito de descontinuidades (todas de primeira espécie) em qualquer intervalo limitado. Em outras palavras, dados
nua se ela tiver apenas um número finito de descontinuidades (todas de primeira espécie) em qualquer intervalo limitado. Em outras palavras, dados 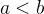 , existem
, existem 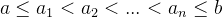 , tais que
, tais que  é cont
é cont nua em cada intervalo aberto
nua em cada intervalo aberto 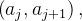
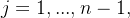 e existem os limites
e existem os limites 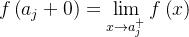 e
e 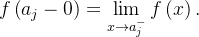
Observação: Toda função cont nua é seccionalmente cont
nua é seccionalmente cont nua.
nua.
Example 91. 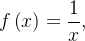
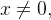 não é seccionalmente cont
não é seccionalmente cont nua, pois sua descontinuidade em
nua, pois sua descontinuidade em 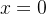 é de segunda espécie.
é de segunda espécie.
Example 92. A função 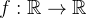 definida por
definida por
não é seccionalmente cont
![\[ f\left( x\right) =\left\{ \begin{array}[c]{l}1,\text { se }x\geq 1\\ \dfrac {1}{n},\text { se }\dfrac {1}{ n+1}\leq x\leq \dfrac {1}{n},\text { }n=1,2,...\\ 0,\text { se }x\leq 0 \end{array} \right. \]](images/img-0782.png)
 nua, apesar de todas as descontinuidades serem de primeira espécie; acontece, porém, que, no intervalo
nua, apesar de todas as descontinuidades serem de primeira espécie; acontece, porém, que, no intervalo 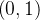 , há um número infinito de tais descontinuidades.
, há um número infinito de tais descontinuidades.
Examples de funções seccionalmente cont nuas:
nuas:
Example 93. A função sinal de  , definida por
, definida por
![\[ signx=\left\{ \begin{array}[c]{c}+1,\text { se }x>0\\ 0,\text { se }x=0\\ -1,\text { se }x<0 \end{array} \right. \]](images/img-0784.png)
Example 94. A função
![\[ f\left( x\right) =\left\{ \begin{array}[c]{c}x+1,\text { se }x\geq 0;\\ 0,\text { se }x<0. \end{array} \right. \]](images/img-0785.png)
Example 95. A função
![\[ f\left( x\right) =\left\{ \begin{array}[c]{c}1,\text { se }0\leq x<\pi \\ 0,\text { se }-\pi \leq x<0\\ \text {e peri\'{o}dica de per\'{\i }odo }2\pi \end{array} \right. \]](images/img-0786.png)
Definition 96. Uma função 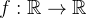 será seccionalmente diferenciável se ela for seccionalmente cont
será seccionalmente diferenciável se ela for seccionalmente cont nua e se a função derivada
nua e se a função derivada 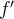 for também seccionalmente cont
for também seccionalmente cont nua.
nua.
Observe que a derivada 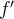 não está definida em todos os pontos: com certeza
não está definida em todos os pontos: com certeza 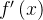 não existe nos pontos
não existe nos pontos  onde
onde  é descont
é descont nua; e mais,
nua; e mais, 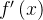 pode não existir, mesmo em alguns pontos onde
pode não existir, mesmo em alguns pontos onde  é cont
é cont nua.
nua.
Example 97. As funções dos exemplos (93) - () anteriores saõ seccionalmente diferenciáveis. Vamos pegar o exemplo (94):
![\[ f\left( x\right) =\left\{ \begin{array}[c]{c}x+1,\text { se }x\geq 0;\\ 0,\text { se }x<0. \end{array} \right. \Rightarrow f^{\prime }\left( x\right) =\left\{ \begin{array}[c]{c}1,\text { se }x\geq 0;\\ 0,\text { se }x<0. \end{array} \right. \]](images/img-0789.png)
Example 98. A seguinte função é cont nua, mas não seccionalmente diferenciável:
nua, mas não seccionalmente diferenciável:
pois nos pontos onde
![\[ f\left( x\right) =\left\{ \begin{array}[c]{c}\sqrt{1-x^{2}},\text { se }\left\vert x\right\vert \leq 1\\ \text {e peri\'{o}dica de per\'{\i }odo 2}\end{array} \right. \]](images/img-0790.png)
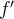 é descont
é descont nua, a descontinuidade é de segunda espécie, pois pela regra da cadeia, temos:
nua, a descontinuidade é de segunda espécie, pois pela regra da cadeia, temos: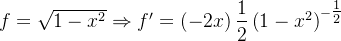 , da
, da ,
, 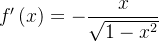 , que é descont
, que é descont nua em
nua em 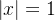 com ela sendo de segunda espécie.
com ela sendo de segunda espécie.
Agora enunciamos um resultado que fornece condições suficientes para a convergência da série de Fourier de uma função 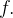
Theorem 99.
(Fourier) Seja 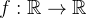 uma função seccionalmente diferenciável e periódica de per
uma função seccionalmente diferenciável e periódica de per odo
odo 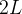 . Então a série de Fourier da função
. Então a série de Fourier da função 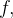 dada em (4.14), converge, em cada ponto
dada em (4.14), converge, em cada ponto  , para:
, para:
![\begin{equation} \dfrac {1}{2}\left[ f\left( x+0\right) +f\left( x-0\right) \right] =\dfrac {1}{2}a_{0}+\sum \limits _{n=1}^{\infty }\left( a_{n}\cos \dfrac {n\pi x}{L}+b_{n}\operatorname{sen}\dfrac {n\pi x}{L}\right) \end{equation}](images/img-0795.png) |
(4.15) |
Exerc cio 1 Calcular a série de Fourier da função
cio 1 Calcular a série de Fourier da função  definida no exemplo 3 acima e traçar o gráfico da função definida por essa série. Compare esse gráfico com o gráfico da função.
definida no exemplo 3 acima e traçar o gráfico da função definida por essa série. Compare esse gráfico com o gráfico da função.
Resolução:
Cálculo dos coeficientes: 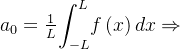 onde o per
onde o per odo da função é
odo da função é 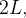 da
da ,
,
![\[ a_{0}=\dfrac {1}{\pi }{\displaystyle \int _{-\pi }^{\pi }} f\left( x\right) dx=\dfrac {1}{\pi }\left( {\displaystyle \int _{-\pi }^{0}} 0dx+ {\displaystyle \int _{0}^{\pi }} 1dx\right) =\dfrac {1}{\pi }\left( \pi -0\right) =1 \]](images/img-0797.png) |
para 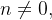 temos:
temos:
![\[ a_{n}=\dfrac {1}{L}{\displaystyle \int _{-L}^{L}} f\left( x\right) \cos \dfrac {n\pi x}{L}dx,n\geq 0;\ \ \ b_{n}=\dfrac {1}{L}{\displaystyle \int _{-L}^{L}} f\left( x\right) \operatorname{sen}\dfrac {n\pi x}{L}dx, \]](images/img-0799.png) |
da ,
,
![\[ a_{n}=\dfrac {1}{\pi } {\displaystyle \int _{-\pi }^{\pi }} f\left( x\right) \cos \left( nx\right) dx=\dfrac {1}{\pi }\left( {\displaystyle \int _{-\pi }^{0}} 0\cos \left( nx\right) dx+ {\displaystyle \int _{0}^{\pi }} 1\cos \left( nx\right) dx\right) , \]](images/img-0800.png) |
resolvendo a integral,temos:
![\[ {\displaystyle \int _{0}^{\pi }} \cos \left( nx\right) dx=\dfrac {1}{\pi }{\displaystyle \int _{0}^{n\pi }} \cos u\dfrac {du}{n} \]](images/img-0801.png) |
![\[ =\dfrac {1}{\pi }\left[ \dfrac {\operatorname{sen}u}{n}\right] _{0}^{n\pi }=\dfrac {1}{n\pi }\left[ \operatorname{sen}\left( n\pi \right) -\operatorname{sen}\left( 0\right) \right] =0 \]](images/img-0802.png) |
e
![\[ b_{n}=\dfrac {1}{\pi }{\displaystyle \int _{-\pi }^{\pi }} f\left( x\right) \operatorname{sen}\left( nx\right) dx=\dfrac {1}{\pi }\left( {\displaystyle \int _{-\pi }^{0}} 0\operatorname{sen}\left( nx\right) dx+ {\displaystyle \int _{0}^{\pi }} 1\operatorname{sen}\left( nx\right) dx\right) , \]](images/img-0803.png) |
de modo análogo para 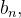 temos
temos
![\[ {\displaystyle \int _{0}^{\pi }} 1\operatorname{sen}\left( nx\right) dx=\dfrac {1}{\pi }{\displaystyle \int _{0}^{n\pi }} \operatorname{sen}u\dfrac {du}{n}=\dfrac {1}{\pi }\left[ -\dfrac {\cos u}{n}\right] _{0}^{n\pi } \]](images/img-0805.png) |
![\[ =-\dfrac {1}{n\pi }\left[ \cos \left( n\pi \right) -\cos \left( 0\right) \right] =\frac{1}{n\pi }\left[ 1-\cos \left( n\pi \right) \right] , \]](images/img-0806.png) |
ou, para 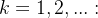
![\[ b_{2k}=\frac{1}{2k\pi }\left[ 1-\cos \left( 2k\pi \right) \right] =0 \]](images/img-0808.png) |
e
![\begin{equation} b_{2k-1}=\frac{1}{\left( 2k-1\right) \pi }\left\{ 1-\cos \left[ \left( 2k-1\right) \right] \pi \right\} =\frac{2}{\left( 2k-1\right) \pi } \label{b2k} \end{equation}](images/img-0809.png) |
(4.16) |
A série de Fourier de  será:
será:
![\[ f\left( x\right) \sim \frac{1}{2}+\sum \limits _{k=1}^{\infty }\frac{2}{\left( 2k-1\right) \pi }\operatorname{sen}\left[ \left( 2k-1\right) x\right] \]](images/img-0810.png) |
Pelo Teorema de Fourier, o gráfico da função definida pela série é dado pela figura 4.3 abaixo.
![\includegraphics[ height=2.3237in, width=5.0981in ]{Figura26.eps}](images/img-0811.png)
Exerc cio 2 Use os resultados do Exerc
cio 2 Use os resultados do Exerc cio 1 para obter uma expressão em série para
cio 1 para obter uma expressão em série para 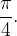
Resolução: No ponto 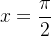 , a série de Fourier é igual a 1, em virtude do Teorema de Fourier:
, a série de Fourier é igual a 1, em virtude do Teorema de Fourier:
![\[ \dfrac {1}{2}\left[ f\left( x+0\right) +f\left( x-0\right) \right] =\dfrac {1}{2}\left[ 1+1\right] =1, \]](images/img-0814.png) |
logo,
![\[ 1=\dfrac {1}{2}+\sum \limits _{k=1}^{\infty }\dfrac {2}{\left( 2k-1\right) \pi }\operatorname{sen}\left[ \left( 2k-1\right) \dfrac {\pi }{2}\right] \]](images/img-0815.png) |
![\[ \frac{1}{2}=\dfrac {2}{\pi }\sum \limits _{k=1}^{\infty }\dfrac {1}{\left( 2k-1\right) }\operatorname{sen}\left[ \left( 2k-1\right) \dfrac {\pi }{2}\right] \]](images/img-0816.png) |
![\[ \dfrac {\pi }{4}=\sum \limits _{k=1}^{\infty }\dfrac {1}{\left( 2k-1\right) }\operatorname{sen}\left[ \left( 2k-1\right) \dfrac {\pi }{2}\right] , \]](images/img-0817.png) |
ou, finalmente,
![\[ \dfrac {\pi }{4}=1-\dfrac {1}{3}+\dfrac {1}{5}-\dfrac {1}{7}+\dfrac {1}{9}-...=\sum \limits _{k=1}^{\infty }\dfrac {\left( -1\right) ^{k-1}}{\left( 2k-1\right) }, \]](images/img-0818.png) |
que é conhecida como uma série de alternada que converge pelo teste de Leibniz.