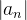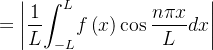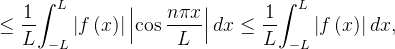4.3 Coeficientes de Fourier
Se uma função 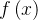 for expressa com:
for expressa com:
| |
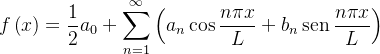 |
|
(4.4) |
é de se esperar que os coeficientes 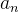 e
e 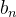 estejam intimamente ligados à função
estejam intimamente ligados à função 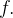
Vamos supor que a igualdade acima se verifique, e que a série em (4.4) convirja uniformemente.
Como consequência da Proposição 1, 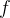 deve ser cont
deve ser cont nua (e portanto, pode ser integrada termo a termo), e deve ser periódica de per
nua (e portanto, pode ser integrada termo a termo), e deve ser periódica de per odo
odo 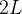 (pois o per
(pois o per odo fundamental de
odo fundamental de 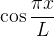 é
é 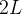 , e
, e 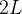 é per
é per odo para as demais funções seno e co-seno que aparecem na série). Assim, usando a Proposição 2, podemos integrar ambos os lados de (4.4) para obter:
odo para as demais funções seno e co-seno que aparecem na série). Assim, usando a Proposição 2, podemos integrar ambos os lados de (4.4) para obter:
| |
 |
|
(4.5) |
por outro lado,
pois,
de modo análogo segue que
segue da igualdade (4.5) e do exposto acima que
segue que
| |
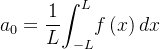 |
|
(4.6) |
Para calcularmos os demais coeficientes usamos as seguintes relações:
| |
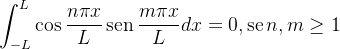 |
|
(4.7) |
| |
![\begin{equation} {\displaystyle \int _{-L}^{L}} \cos \dfrac {n\pi x}{L}\cos \dfrac {m\pi x}{L}dx=\left\{ \begin{array}[c]{l}L,\text { se }n=m\geq 1\\ 0,\text { se }n\neq m,n,m\geq 1 \end{array} \right.\label{rel2} \end{equation}](images/img-0740.png) |
|
(4.8) |
| |
![\begin{equation} {\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {n\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx=\left\{ \begin{array}[c]{l}L,\text { se }n=m\geq 1\\ 0,\text { se }n\neq m,n,m\geq 1 \end{array} \right.\label{rel3} \end{equation}](images/img-0741.png) |
|
(4.9) |
por questões de esclarecimento vamos provar uma dessas relações, para 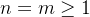 temos:
temos:
Analogamente mostram-se as outras relações.
Agora, multiplicando (4.4) por 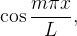 com
com  fixo, e integrando de
fixo, e integrando de 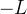 a
a 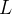 , obtemos:
, obtemos:
Do somatório acima obtemos
Usando as relações (4.7), (4.8) e (4.9) expostas acima concluímos que:
o que nos dá
| |
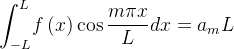 |
|
(4.10) |
De modo análogo, multiplicando (4.4) por 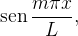 com
com  fixo, e integrando de
fixo, e integrando de 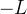 a
a 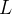 , obtemos:
, obtemos:
daí
Novamente das relações (4.7), (4.8) e (4.9) temos:
segue que
| |
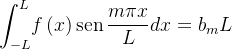 |
|
(4.11) |
Finalmente, de (4.6), (4.10) e (4.11) obtemos:
| |
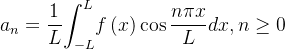 |
|
(4.12) |
| |
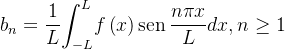 |
|
(4.13) |
Definition 89. Seja 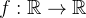 uma função periódica de per
uma função periódica de per odo
odo 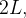 integrável e absolutamente integrável em cada intervalo limitado; em particular,
integrável e absolutamente integrável em cada intervalo limitado; em particular, 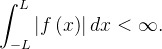 Os números
Os números 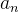 , para
, para 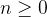 , e
, e 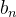 , para
, para 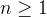 , dados em (4.12) e (4.13) são definidos como os coeficientes de Fourier da função
, dados em (4.12) e (4.13) são definidos como os coeficientes de Fourier da função 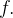 (A exigência da integrabilidade e integrabilidade absoluta de
(A exigência da integrabilidade e integrabilidade absoluta de 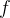 é necessária para que as expressões (4.12) e (4.13) façam sentido.)
é necessária para que as expressões (4.12) e (4.13) façam sentido.)
Obs.:
o que dá sentido à integral.
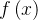 for expressa com:
for expressa com: 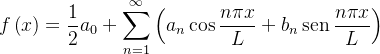
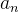 e
e 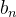 estejam intimamente ligados à função
estejam intimamente ligados à função 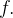
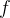 deve ser cont
deve ser cont nua (e portanto, pode ser integrada termo a termo), e deve ser periódica de per
nua (e portanto, pode ser integrada termo a termo), e deve ser periódica de per odo
odo 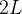 (pois o per
(pois o per odo fundamental de
odo fundamental de 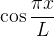 é
é 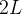 , e
, e 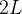 é per
é per odo para as demais funções seno e co-seno que aparecem na série). Assim, usando a Proposição 2, podemos integrar ambos os lados de (4.4) para obter:
odo para as demais funções seno e co-seno que aparecem na série). Assim, usando a Proposição 2, podemos integrar ambos os lados de (4.4) para obter: 
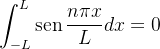
![\begin{equation*} {\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {n\pi x}{L}dx=\dfrac {L}{n\pi }{\displaystyle \int _{-n\pi }^{n\pi }}\operatorname{sen}udu=-\dfrac {L}{n\pi }\left( \cos u\right) ]_{-n\pi }^{n\pi }=0 \end{equation*}](images/img-0735.png)
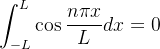
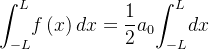
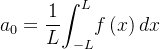
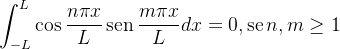
![\begin{equation} {\displaystyle \int _{-L}^{L}} \cos \dfrac {n\pi x}{L}\cos \dfrac {m\pi x}{L}dx=\left\{ \begin{array}[c]{l}L,\text { se }n=m\geq 1\\ 0,\text { se }n\neq m,n,m\geq 1 \end{array} \right.\label{rel2} \end{equation}](images/img-0740.png)
![\begin{equation} {\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {n\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx=\left\{ \begin{array}[c]{l}L,\text { se }n=m\geq 1\\ 0,\text { se }n\neq m,n,m\geq 1 \end{array} \right.\label{rel3} \end{equation}](images/img-0741.png)
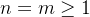 temos:
temos: ![\[ {\displaystyle \int _{-L}^{L}} \cos ^{2}\dfrac {n\pi x}{L}dx=\dfrac {L}{n\pi }{\displaystyle \int _{-n\pi }^{n\pi }\cos ^{2}udu}=\dfrac {L}{2n\pi } {\displaystyle \int _{-n\pi }^{n\pi }} \left( \cos 2u+1\right) du \]](images/img-0743.png)
![\[ =\dfrac {L}{2n\pi }\left[ \left( \frac{1}{2}\operatorname{sen}2u\right) +\left( u\right) \right]_{-n\pi }^{n\pi } =\dfrac {L}{2n\pi }\left[ n\pi -\left( -n\pi \right) \right] =\dfrac {L}{2n\pi }\left[ 2n\pi \right] =L \]](images/img-0744.png)
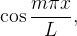 com
com  fixo, e integrando de
fixo, e integrando de 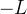 a
a 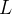 , obtemos:
, obtemos: ![\[ {\displaystyle \int _{-L}^{L}} f\left( x\right) \cos \dfrac {m\pi x}{L}dx=\frac{1}{2}a_{0}{\displaystyle \int _{-L}^{L}} \cos \dfrac {m\pi x}{L}dx+ \]](images/img-0749.png)
![\[ +\sum \limits _{n=1}^{\infty }\left( a_{n} {\displaystyle \int _{-L}^{L}} \cos \dfrac {n\pi x}{L}\cos \dfrac {m\pi x}{L}dx+b_{n} {\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {n\pi x}{L}\cos \dfrac {m\pi x}{L}dx\right) \]](images/img-0750.png)
![\[ {\displaystyle \int _{-L}^{L}} f\left( x\right) \cos \dfrac {m\pi x}{L}dx=\frac{1}{2}a_{0} {\displaystyle \int _{-L}^{L}} \cos \dfrac {m\pi x}{L}dx \]](images/img-0751.png)
![\[ +(a_{1}{\displaystyle \int _{-L}^{L}} \cos \dfrac {\pi x}{L}\cos \dfrac {m\pi x}{L}dx+b_{1}{\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {\pi x}{L}\cos \dfrac {m\pi x}{L}dx+... \]](images/img-0752.png)
![\[ +a_{m} {\displaystyle \int _{-L}^{L}} \cos \dfrac {m\pi x}{L}\cos \dfrac {m\pi x}{L}dx+b_{m} {\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {m\pi x}{L}\cos \dfrac {m\pi x}{L}dx+...) \]](images/img-0753.png)
![\[ {\displaystyle \int _{-L}^{L}} f\left( x\right) \cos \dfrac {m\pi x}{L}dx=0+\left( 0+...+a_{m}L+b_{m}0+...+0+...\right) \]](images/img-0754.png)
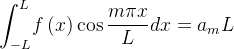
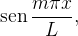 com
com  fixo, e integrando de
fixo, e integrando de 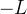 a
a 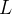 , obtemos:
, obtemos: ![\[ {\displaystyle \int _{-L}^{L}} f\left( x\right) \operatorname{sen}\dfrac {m\pi x}{L}dx=\frac{1}{2}a_{0}{\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {m\pi x}{L}dx+ \]](images/img-0757.png)
![\[ +\sum \limits _{n=1}^{\infty }\left( a_{n}{\displaystyle \int _{-L}^{L}} \cos \dfrac {n\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx+b_{n}{\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {n\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx\right) \]](images/img-0758.png)
![\[ {\displaystyle \int _{-L}^{L}} f\left( x\right) \operatorname{sen}\dfrac {m\pi x}{L}dx=\frac{1}{2}a_{0}{\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {m\pi x}{L}dx \]](images/img-0759.png)
![\[ +(a_{1} {\displaystyle \int _{-L}^{L}} \cos \dfrac {\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx+b_{1} {\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx+... \]](images/img-0760.png)
![\[ +a_{m} {\displaystyle \int _{-L}^{L}} \cos \dfrac {m\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx+b_{m} {\displaystyle \int _{-L}^{L}} \operatorname{sen}\dfrac {m\pi x}{L}\operatorname{sen}\dfrac {m\pi x}{L}dx+...) \]](images/img-0761.png)
![\[ {\displaystyle \int _{-L}^{L}} f\left( x\right) \operatorname{sen}\dfrac {m\pi x}{L}dx=0+\left( 0+...+a_{m}0+b_{m}L+...+0+...\right) \]](images/img-0762.png)
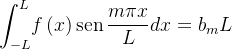
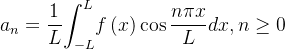
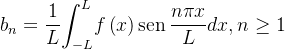
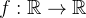 uma função periódica de per
uma função periódica de per odo
odo 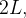 integrável e absolutamente integrável em cada intervalo limitado; em particular,
integrável e absolutamente integrável em cada intervalo limitado; em particular, 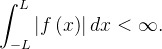 Os números
Os números 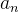 , para
, para 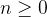 , e
, e 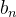 , para
, para 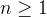 , dados em (4.12) e (4.13) são definidos como os coeficientes de Fourier da função
, dados em (4.12) e (4.13) são definidos como os coeficientes de Fourier da função 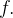 (A exigência da integrabilidade e integrabilidade absoluta de
(A exigência da integrabilidade e integrabilidade absoluta de 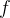 é necessária para que as expressões (4.12) e (4.13) façam sentido.)
é necessária para que as expressões (4.12) e (4.13) façam sentido.)