| Séries e Equações Diferenciais Ordinárias |
 mpares
mparesDefinition 100. Uma função 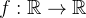 é par se
é par se 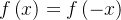 , para todo
, para todo 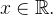 (Isso significa que o gráfico da função
(Isso significa que o gráfico da função 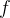 é simétrico com relação ao eixo dos
é simétrico com relação ao eixo dos  ).
).
Definition 101. Uma função 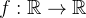 é
é  mpar se
mpar se 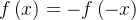 , para todo
, para todo 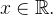 (Isso significa que o gráfico da função
(Isso significa que o gráfico da função 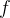 é simétrico com relação à origem).
é simétrico com relação à origem).
Example 102. funções pares: 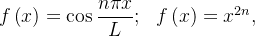 para
para 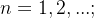 outro:
outro: 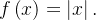
Example 103. funções  mpares:
mpares: 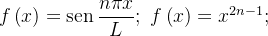 para
para 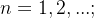 outro:
outro: 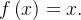
Proposition 104. A soma de duas funções pares é uma função par A soma de duas funções O produto de duas funções pares é uma função par. O produto de duas funções O produto de uma função par por uma função
 mpares é uma função
mpares é uma função  mpar.
mpar.  mpares é uma função par.
mpares é uma função par.  mpar é uma função
mpar é uma função  mpar.
mpar.
Demonstração:
 Sejam
Sejam 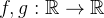 funções pares
funções pares
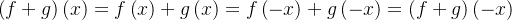
 Sejam
Sejam 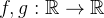 funções
funções  mpares
mpares
![$\left( f+g\right) \left( x\right) =f\left( x\right) +g\left( x\right) =-f\left( -x\right) +\left[ -g\left( -x\right) \right] =-\left[ f\left( -x\right) +g\left( -x\right) \right] =-\left( f+g\right) \left( -x\right) $](images/img-0831.png)
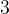 Sejam
Sejam 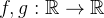 funções pares:
funções pares:
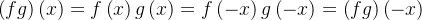
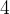 Sejam
Sejam 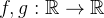 funções
funções  mpares:
mpares:
![$\left( fg\right) \left( x\right) =f\left( x\right) g\left( x\right) =\left[ -f\left( -x\right) \right] \left[ -g\left( -x\right) \right] =\left[ f\left( -x\right) g\left( -x\right) \right] =\left( fg\right) \left( -x\right) $](images/img-0835.png)
 Sejam
Sejam 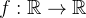 uma função par e
uma função par e 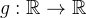 uma função
uma função  mpar:
mpar:
![$\left( fg\right) \left( x\right) =f\left( x\right) g\left( x\right) =f\left( -x\right) \left[ -g\left( -x\right) \right] =-\left[ f\left( -x\right) g\left( -x\right) \right] =-\left( fg\right) \left( -x\right) $](images/img-0838.png)
Proposition 105. 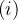 Seja
Seja 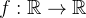 uma função par que é integrável em qualquer intervalo limitado. Então:
uma função par que é integrável em qualquer intervalo limitado. Então:
![\[ {\displaystyle \int _{-L}^{L}} f=2{\displaystyle \int _{0}^{L}} f \]](images/img-0840.png)
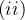 Se
Se 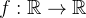 é uma função
é uma função  mpar e integrável em qualquer intervalo limitado. Então:
mpar e integrável em qualquer intervalo limitado. Então:
![\[ {\displaystyle \int _{-L}^{L}} f=0 \]](images/img-0842.png)
Demonstração:Seja 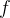 uma função par e considere a integral
uma função par e considere a integral 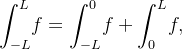 temos que para
temos que para 
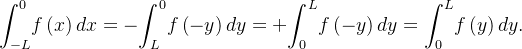
isso mostra que se 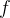 é par então
é par então
![\[ {\displaystyle \int _{-L}^{L}} f=2{\displaystyle \int _{0}^{L}} f \]](images/img-0840.png) |
Analogamente, seja 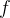 uma função
uma função  mpar temos que
mpar temos que 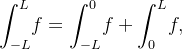 e para
e para 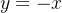 teremos
teremos
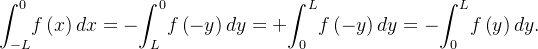
que mostra
![\[ {\displaystyle \int _{-L}^{L}} f=0 \]](images/img-0842.png) |
Da proposição anterior podemos estabelecer os seguintes resultados sobre as séries de fourier de funções pares e  mpares.
mpares.
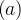 Se
Se 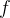 for uma função par, periódica de per
for uma função par, periódica de per odo
odo 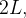 integrável e absolutamente integrável, então:
integrável e absolutamente integrável, então:
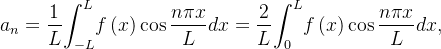
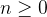 ,
, pois o produto de duas funções pares é uma função par. E,
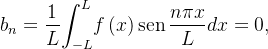
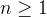 ,
, pois o produto de uma função par e uma função  mpar é uma função
mpar é uma função  mpar.
mpar.
Portanto, a série de Fourier de uma função par é uma série de co-senos.
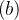 Se
Se 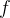 for uma função
for uma função  mpar, periódica de per
mpar, periódica de per odo
odo 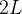 , integrável e absolutamente integrável, então:
, integrável e absolutamente integrável, então:
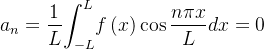 ,
, pois o produto de uma função par e uma função  mpar é uma função
mpar é uma função  mpar. E,
mpar. E,
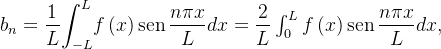
pois o produto de duas funções  mpares é uma função par.
mpares é uma função par.
Assim, a série de Fourier de uma função  mpar é uma série de senos.
mpar é uma série de senos.