| Séries e Equações Diferenciais Ordinárias |
Definition 85. Uma função 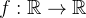 é periódica de per
é periódica de per odo
odo 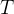 se
se 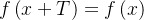 para todo
para todo 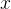 .
.
Example 86.
A função  é periódica de per
é periódica de per odo
odo  . Observe a figura 4.1.
. Observe a figura 4.1.
![\includegraphics[ height=1.3759in, width=2.1465in ]{Figura16.eps}](images/img-0699.png)
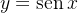
Example 87.
A função ![$f\left( x\right) =x-\left[ x\right] ,$](images/img-0701.png) onde
onde ![$\left[ x\right] $](images/img-0702.png) representa o maior inteiro, menor do que ou igual a
representa o maior inteiro, menor do que ou igual a 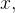 é periódica de per
é periódica de per odo
odo 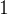 . Veja o gráfico de
. Veja o gráfico de 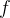 dado pela figura 4.2.
dado pela figura 4.2.
![\includegraphics[ height=1.7772in, width=4.0188in ]{Figura13.eps}](images/img-0704.png)
![$f(x)=x-[x]$](images/img-0705.png)
Observação:
Se 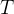 é um per
é um per odo para a função
odo para a função 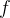 , então
, então 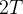 também é um per
também é um per odo, pois:
odo, pois:
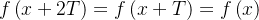 |
E em geral, 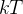 é um per
é um per odo, onde
odo, onde 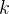 é um inteiro. Para
é um inteiro. Para 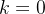 , temos que
, temos que 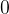 é um per
é um per odo da
odo da 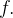 Mas isso não tem interesse pois
Mas isso não tem interesse pois 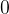 é per
é per odo de qualquer função. O menor per
odo de qualquer função. O menor per odo positivo é chamado o per
odo positivo é chamado o per odo fundamental.
odo fundamental.
Example 88. O per odo fundamental
odo fundamental 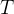 da função
da função 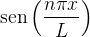 pode ser determinado do seguinte modo. Devemos ter:
pode ser determinado do seguinte modo. Devemos ter:
Usando a seguinte propriedade trigonométrica,
![\[ \operatorname{sen}\dfrac {n\pi \left( x+T\right) }{L}=\operatorname{sen}\dfrac {n\pi x}{L},\forall x\in \mathbb {R}. \]](images/img-0713.png)
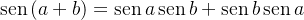 , devemos ter:
, devemos ter:
Fazendo
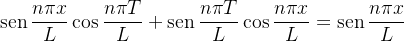
(4.1)
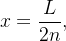 na igualdade acima obtemos:
na igualdade acima obtemos:
O que implica:
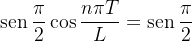
, e da
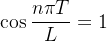
(4.2)
 , usando a identidade:
, usando a identidade: 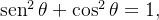 obtemos:
obtemos:
Como estamos interessados no menor valor positivo de
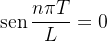
(4.3)
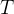 que satisfaça (4.2) e (4.3), simultaneamente, então
que satisfaça (4.2) e (4.3), simultaneamente, então 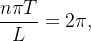 isto é, o per
isto é, o per odo fundamental de
odo fundamental de 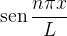 é:
é: 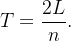 (De maneira análoga obtemos que o per
(De maneira análoga obtemos que o per odo fundamental de
odo fundamental de 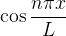 é também
é também 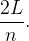 )
)