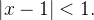| Séries e Equações Diferenciais Ordinárias |
Quando uma função é representada por uma série de potências então podemos ter
![\[ f(x)=\sum _{n=0}^{\infty } a_ n x^ n=a_0+a_1 x+a_2 x^2+\cdots + a_ n x^ n+\cdots \]](images/img-0594.png) |
Levantamos então as seguintes questões: que relação há entre 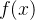 e os coeficientes da série
e os coeficientes da série 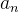 ? Em que situação essa série representa realmente a função
? Em que situação essa série representa realmente a função 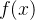 ? Em relação à primeira questão temos que se
? Em relação à primeira questão temos que se 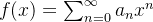 e se
e se 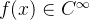 então
então 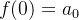 e, como
e, como 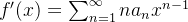 então
então 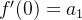 , como
, como 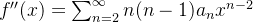 então
então 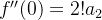 , e assim por diante, seguindo esse mesmo raciocínio obtemos
, e assim por diante, seguindo esse mesmo raciocínio obtemos 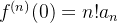 então podemos concluir que
então podemos concluir que
![\[ f(x)=f(0)+f’(0)x+\dfrac {f”(0)}{2!}x^2 +\cdots +\dfrac {f^{(n)}(0)}{n!}x^ n+\cdots \]](images/img-0603.png) |
essa série é conhecida como série de Maclaurin da função  . A série de Taylor de
. A série de Taylor de  em torno de um ponto
em torno de um ponto 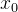 é
é
![\[ f(x)=f(x_0)+f’(x_0)(x-x_0)+\dfrac {f”(x_0)}{2!}(x-x_0)^2 +\cdots +\dfrac {f^{(n)}(x_0)}{n!}(x-x_0)^ n+\cdots \]](images/img-0604.png) |
onde os 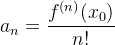 , para todo
, para todo 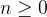 , aqui usa-se a convenção de que
, aqui usa-se a convenção de que 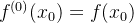 . A série de Maclaurin de uma função
. A série de Maclaurin de uma função  nada mais é que a sua série de Taylor em torno do ponto
nada mais é que a sua série de Taylor em torno do ponto 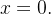
Example 77. Achar a série de Maclaurin da função 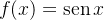 .
.
Solução: Temos que
![\[ \begin{cases} f(x)=\operatorname{sen}x \Rightarrow f(0)=\operatorname{sen}0=0\\ f’(x)=\cos x \Rightarrow f’(0)=\cos 0=1\\ f”(x)=-\operatorname{sen}x \Rightarrow f”(0)=-\operatorname{sen}0=0\\ f”’(x)=-\cos x \Rightarrow f”’(0)=-\cos 0=-1\\ f^{(iv)}(x)=\operatorname{sen}x \Rightarrow f^{(iv)}(0)=\operatorname{sen}0=0 \end{cases} \]](images/img-0610.png) |
só os termos ímpares são diferentes de zero, analisemos esses termos
![\[ \begin{cases} f^{(1)}(0)=f^{(2.0+1)}(0)=(-1)^0=1\\ f^{(3)}(0)=f^{(2.1+1)}(0)=(-1)^1=-1\\ f^{(5)}(0)=f^{(2.2+1)}(0)=(-1)^2=1\\ \vdots \\ f^{(2.k+1)}(0)=(-1)^ k \end{cases} \]](images/img-0611.png) |
assim
![\[ \operatorname{sen}x=x-\dfrac {x^3}{3!}+\dfrac {x^5}{5!}-\cdots +\dfrac {(-1)^ n x^{2n+1}}{(2n+1)!}+\cdots \]](images/img-0612.png) |
Essa é a série de Maclaurin da função 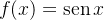 . Com a série de Maclaurin da função
. Com a série de Maclaurin da função 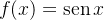 podemos encontrar a série de Maclaurin da função
podemos encontrar a série de Maclaurin da função 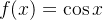 , por derivação termo a termo,
, por derivação termo a termo,
![\[ \cos x=\dfrac {d}{dx}(\operatorname{sen}x)=1-\dfrac {x^2}{2!}+\dfrac {x^4}{4!}-\cdots +\dfrac {(-1)^ n x^{2n}}{(2n)!}+\cdots \]](images/img-0614.png) |
Example 78. Encontre a série de Taylor da função 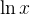 em torno de
em torno de 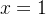 .
.
Solução: Temos
![\[ \begin{cases} f(x)=\ln x \Rightarrow f(1)=\ln 1=0\\ f’(x)=\dfrac {1}{x} \Rightarrow f’(1)=1\\ f”(x)=\dfrac {-1}{x^2} \Rightarrow f”(1)=-1\\ f”’(x)=\dfrac {2}{x^3} \Rightarrow f”’(1)=2\\ f^{(iv)}(x)=-\dfrac {3!}{x^4} \Rightarrow f^{(iv)}(1)=-3!\\ \vdots \\ f^{(n)}(x)=(-1)^{n-1}\dfrac {(n-1)!}{x^ n} \Rightarrow f^{(n)}(1)=(-1)^{n-1} (n-1)! \end{cases} \]](images/img-0616.png) |
logo,
![\[ \ln x=(x-1)-\dfrac {(x-1)^2}{2}+\dfrac {(x-1)^3}{3}-\dfrac {(x-1)^4}{4}+\cdots +\dfrac {(-1)^ n(x-1)^ n}{n}+\cdots \]](images/img-0617.png) |
com