| Séries e Equações Diferenciais Ordinárias |
Binômio de Newton
![\[ (x+y)^ k=x^ k +kx^{k-1}y+\dfrac {k(k-1)}{2!} x^{k-2}y^2+\cdots +y^ k \]](images/img-0670.png) |
ou simbolicamente,
![\[ (x+y)^ k=\sum _{j=0}^ k {k \choose j} x^ j y^{k-j}; \]](images/img-0671.png) |
onde
![\[ {k \choose j} =\dfrac {k!}{j!(k-j)!} \]](images/img-0672.png) |
fazendo nesta fórmula 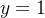 , obtemos
, obtemos
![\[ (1+x)^ k=1+kx+\dfrac {k(k-1)}{2!}x^2+\cdots +\dfrac {k(k-1)\cdots (k-j+1)}{j!}x^ j+\cdots +x^ k \]](images/img-0674.png) |
Motivado por essa fórmula, procuramos um desenvolvimento em série de potências para a função 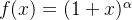 , onde
, onde 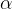 é um número real qualquer.A série binomial é definida como
é um número real qualquer.A série binomial é definida como
![\[ 1+\alpha x+\dfrac {\alpha (\alpha -1)}{2!}x^2+\cdots +\dfrac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}x^ n+\cdots \]](images/img-0677.png) |
o n-ésimo termo dessa série é
![\[ a_ n=\dfrac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}x^ n \]](images/img-0678.png) |
logo,
![\[ \lim _{n\to \infty } \left| \dfrac {a_{n+1}}{a_ n}\right|=\lim _{n\to \infty } |x| \dfrac {|\alpha -n|}{n+1}=|x| \]](images/img-0679.png) |
portanto, a série binomial converge absolutamente quando  e diverge se
e diverge se 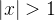 . Se tal série converge para uma função
. Se tal série converge para uma função 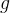 então devemos ter que
então devemos ter que
![\[ g(x)=1+\sum _{n=1}^{\infty } \dfrac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}x^ n \]](images/img-0682.png) |
e, por derivação termo a termo
![\[ g’(x)=\alpha +\alpha (\alpha -1)x+\cdots +\dfrac {n\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}x^{n-1} +\cdots \]](images/img-0683.png) |
desse modo,
![\[ g’(x)+xg’(x)=\alpha g(x) \]](images/img-0684.png) |
ou
![\[ (1+x)g’(x)-\alpha g(x)=0 \]](images/img-0685.png) |
daí
![\[ \dfrac {d}{dx}\left[ \dfrac {g(x)}{(1+x)^{\alpha }}\right]=\dfrac {(1+x)g’(x)-\alpha g(x)}{(1+x)^{\alpha +1}} \]](images/img-0686.png) |
ou
![\[ \dfrac {g(x)}{(1+x)^{\alpha }}=c \]](images/img-0687.png) |
e como 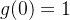 então
então 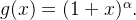
Example 84. Ache a série binomial da função 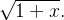
Solução: Como 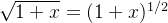 então
então
![\[ (1+x)^{1/2}=1+\dfrac {1}{2}x-\dfrac {1}{8}x^2+\cdots +\dfrac {\dfrac {1}{2}(\dfrac {1}{2}-1)\cdots (\dfrac {1}{2}-n+1)}{n!}x^ n+\cdots \]](images/img-0692.png) |
![\[ =1+\dfrac {1}{2}x-\dfrac {1}{8}x^2+\cdots +(-1)^ n \dfrac {1.3.\cdots (2n-3)}{2^ n n!}x^ n+\cdots \]](images/img-0693.png) |