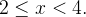| Séries e Equações Diferenciais Ordinárias |
Uma série de potências de  é uma série do tipo
é uma série do tipo
![\[ \sum _{n=0}^{\infty } a_ n x^ n=a_0 + a_1 x+a_2 x^2+\cdots +a_ n x^ n+\cdots \]](images/img-0496.png) |
Example 68. A série
é uma série de potências de
![\[ \sum _{n=0}^{\infty } x^ n=1+x+x^2+\cdots +x^ n+\cdots \]](images/img-0497.png)
 . Observe que ela é uma série geométrica de razão
. Observe que ela é uma série geométrica de razão  . Como a série geométrica só converge se
. Como a série geométrica só converge se  então a série
então a série 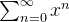 só converge se
só converge se 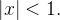 Neste caso, sua soma é
Neste caso, sua soma é 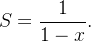 Podemos então afirmar que
Podemos então afirmar que
![\[ \dfrac {1}{1-x}=1+x+x^2+\cdots +x^ n+\cdots , \, \, \, |x|<1. \]](images/img-0502.png)
Dada uma série de potências de  ,
, 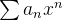 , usando o teste da razão temos que
, usando o teste da razão temos que
![\[ \lim _{n\to \infty } \left|\dfrac {a_{n+1}x^{n+1}}{a_ n x^ n}\right|=|x| \lim _{n\to \infty } \left|\dfrac {a_{n+1}}{a_ n}\right|=|x|l<1 \]](images/img-0504.png) |
logo, 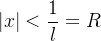 ,
, 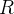 é o raio de convergência da série
é o raio de convergência da série 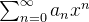 .
.
Theorem 69. Seja 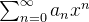 uma série de potências de
uma série de potências de  . Se
. Se 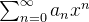 converge para um certo
converge para um certo 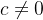 e diverge para um certo
e diverge para um certo 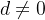 com
com 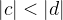 . Então
. Então 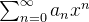 converge absolutamente para todo
converge absolutamente para todo  tal que
tal que 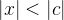 e diverge para todo
e diverge para todo  tal que
tal que 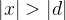 .
.
Seja a série 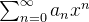 tal que ela converge para
tal que ela converge para  e diverge para
e diverge para 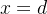 com
com 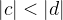 . Considere
. Considere  tal que
tal que 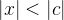 temos que
temos que
![\[ \sum _{n=0}^{\infty } |a_ n ||x|^ n=\sum _{n=0}^{\infty } |a_ n c^ n| \left(\frac{|x|}{|c|}\right)^ n \]](images/img-0515.png) |
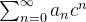 converge então devemos ter que
converge então devemos ter que 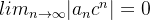 , podemos então tomar
, podemos então tomar 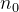 tal que
tal que 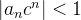 para todo
para todo  desse modo,
desse modo, ![\[ |a_ n||x|^ n= |a_ n c^ n| \left(\frac{|x|}{|c|}\right)^ n<\left(\frac{|x|}{|c|}\right)^ n,\, \, \, \forall n>n_0 \]](images/img-0519.png) |
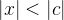 então
então 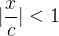 e a série
e a série 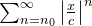 é uma série geométrica convergente. Desse modo, a série
é uma série geométrica convergente. Desse modo, a série 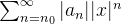 converge, o que implica que a série
converge, o que implica que a série 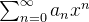 converge absolutamente para todo
converge absolutamente para todo 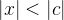 . Agora suponha que
. Agora suponha que  seja tal que
seja tal que 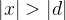 se, por absurdo, supomos que exista algum
se, por absurdo, supomos que exista algum 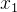 com
com 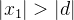 e
e 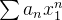 convirja, então pelo que acabamos de mostrar essa série deve convergir para todo
convirja, então pelo que acabamos de mostrar essa série deve convergir para todo  tal que
tal que 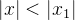 assim, como,
assim, como, 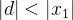 então
então 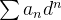 converge, o que é um absurdo. Então para todo
converge, o que é um absurdo. Então para todo  tal que
tal que 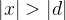 a série
a série 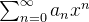 diverge.
diverge. Theorem 70. Seja A série converge somente para A série converge para todo Existe 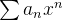 uma série de potências de
uma série de potências de  . Então somente uma das alternativas abaixo deve ocorrer.
. Então somente uma das alternativas abaixo deve ocorrer.
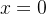 (R=
(R=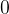 )
)  real. (R=
real. (R=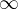 )
) 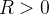 tal que a série
tal que a série 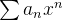 converge para todo
converge para todo  tal que
tal que 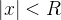 e diverge para todo
e diverge para todo  tal que
tal que 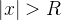 .
.
Se não ocorre a primeira nem a segunda situação então existe um 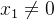 onde
onde 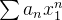 converge e um
converge e um 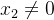 com
com 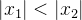 onde
onde 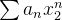 diverge. Seja
diverge. Seja
![\[ S=\{ x\in \mathbb {R}| \sum a_ n x^ n \quad \mbox{converge}\} \]](images/img-0540.png) |
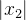 é uma cota superior de
é uma cota superior de 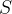 , tomemos então
, tomemos então 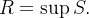 Provemos que se
Provemos que se 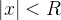 então
então 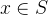 . De fato, se
. De fato, se 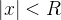 então
então  não pode ser cota superior de
não pode ser cota superior de 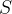 já que
já que 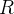 é a menor das cotas superiores, então deve ter um elemento
é a menor das cotas superiores, então deve ter um elemento 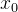 de
de 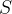 tal que
tal que 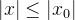 então pelo teorema anterior
então pelo teorema anterior 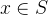 . Também se
. Também se  não pertencesse a
não pertencesse a 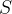 então
então 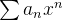 divergiria e
divergiria e  seria uma cota superior de
seria uma cota superior de 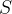 o que contradiz o fato de
o que contradiz o fato de 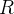 ser a menor delas, já que
ser a menor delas, já que 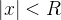 . Por outro lado, se
. Por outro lado, se 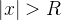 então
então  deve divergir, pois se
deve divergir, pois se  convergisse
convergisse 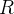 não seria uma cota superior de
não seria uma cota superior de 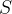 o que é absurdo já que
o que é absurdo já que 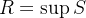 .
. 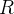 é o raio de convergência da série
é o raio de convergência da série 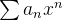 . Já o intervalo de convergência da série é um dos seguintes intervalos:
. Já o intervalo de convergência da série é um dos seguintes intervalos:
![\[ (-R, R),\, \, (-R,R],\, \, [-R,R), \, \, [-R,R] \]](images/img-0548.png) |
fora desses intervalos a série sempre diverge. E o intervalo 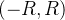 é sempre o intervalo de convergência absoluta da série.
é sempre o intervalo de convergência absoluta da série.
Theorem 71. Seja 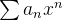 uma série de potências de
uma série de potências de  . Se essa série tem raio de convergência
. Se essa série tem raio de convergência 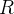 . Então ela pode ser derivada termo a termo ou integrada termo a termo, isto é,
. Então ela pode ser derivada termo a termo ou integrada termo a termo, isto é,
![\[ \dfrac {d}{dx}\left(\sum _{n=0}^{\infty } a_ n x^ n\right)=\dfrac {d}{dx}\left(a_0+a_1 x+a_2 x^2+\cdots +a_ n x^ n+\cdots \right) \]](images/img-0550.png)
e
![\[ =a_1 +2a_2 x+3a_3 x^2 + \cdots +n a_ n x^{n-1}+\cdots =\sum _{n=1}^{\infty } n a_ n x^{n-1} \]](images/img-0551.png)
essas novas séries obtidas têm o mesmo raio de convergência da série original.
![\[ \int _0^ x \left(\sum _{n=0}^{\infty } a_ n t^ n\right) dt=\sum _{n=0}^{\infty } \int _0^ x t^ n dt=\sum _{n=0}^{\infty } \dfrac {a_ n x^{n+1}}{n+1} \]](images/img-0552.png)
Example 72. Obtenha uma série de potências de  que represente a função
que represente a função 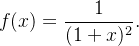
Solução: Observe que
![\[ \dfrac {d}{dx}\left(\dfrac {1}{1+x}\right)=-\dfrac {1}{(1+x)^2} \]](images/img-0554.png) |
como
![\[ \dfrac {1}{1+x}=1-x+x^2-\cdots +(-1)^ n x^ n+\cdots \]](images/img-0555.png) |
usando o teorema 71 obtemos
![\[ -\dfrac {1}{(1+x)^2}=\dfrac {d}{dx}\left(\dfrac {1}{1+x}\right)=-1+2x-3x^2+\cdots +(-1)^ n n x^{n-1}+\cdots \, \, \, |x|<1. \]](images/img-0556.png) |
Example 73. Obtenha uma série de potências de  que represente a função
que represente a função 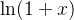 .
.
Solução: Note que
![\[ \ln (1+x)=\int _0^ x \dfrac {1}{1+t}dt \]](images/img-0558.png) |
como
![\[ \dfrac {1}{1+t}=\sum _{n=0}^{\infty } (-1)^ n t^ n, \, \, \, |t|<1 \]](images/img-0559.png) |
o que nos leva a
![\[ \ln x=\sum _{n=0}^{\infty } (-1)^ n\dfrac {x^{n+1}}{n+1},\, \, \, |x|<1 \]](images/img-0560.png) |
O intervalo de convergência dessa série é ![$(-1,1]$](images/img-0561.png) . Isso, porque quando escolhemos
. Isso, porque quando escolhemos 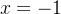 na série de
na série de 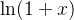 obtemos a série numérica
obtemos a série numérica 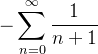 que é divergente, por outro lado, se fazemos
que é divergente, por outro lado, se fazemos 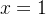 na série de
na série de 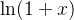 obtemos a série
obtemos a série 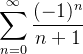 que converge pelo teste de Leibniz.
que converge pelo teste de Leibniz.
Example 74. A série 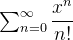 é absolutamente convergente para todo
é absolutamente convergente para todo  real. Que função essa série representa?
real. Que função essa série representa?
Solução:De fato,vemos que
![\[ \lim _{n \to \infty } \left| \dfrac {x^{n+1}}{(n+1)!}\dfrac {n!}{x^ n} \right|=\lim _{n \to \infty } \dfrac {|x|}{n+1}=0<1 \]](images/img-0567.png) |
então pelo teste da razão essa série converge absolutamente para todo  real. Suponha que a série acima represente uma função
real. Suponha que a série acima represente uma função 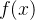 , ou seja,
, ou seja, 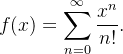 Derivando a função
Derivando a função 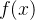 obtemos
obtemos
![\[ f’(x)=\sum _{n=1}^{\infty } n \dfrac {x^{n-1}}{n!} \]](images/img-0569.png) |
ou
![\[ f’(x)=\sum _{n=1}^{\infty } \dfrac {x^{n-1}}{(n-1)!} \]](images/img-0570.png) |
ou ainda
![\[ f’(x)=f(x) \]](images/img-0571.png) |
daí
![\[ \dfrac {f’(x)}{f(x)}=1 \]](images/img-0572.png) |
integrando a igualdade acima obtemos
![\[ \ln f(x)=x+c_0 \]](images/img-0573.png) |
ou
![\[ f(x)=Ce^ x,\, \, \, (C=e^ c_0 \, \, \, \mbox{é uma constante}) \]](images/img-0574.png) |
como 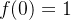 obtemos
obtemos 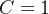 e
e 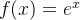 , portanto,
, portanto, 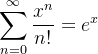 .
.
Uma série de potências de  é uma série do tipo
é uma série do tipo
![\[ \sum _{n=0}^{\infty } a_ n (x-x_0)^ n=a_0+a_1 (x-x_0) + a_2 (x-x_0)^2+\cdots +a_ n (x-x_0)^ n+\cdots \]](images/img-0580.png) |
Todos os resultados que obtivemos para as séries de potências de  são válidos para as séries de potências de
são válidos para as séries de potências de  com as devidas adaptações.
com as devidas adaptações.
Example 75. Da série
obtemos
![\[ \dfrac {1}{1+x}=\sum _{n=0}^{\infty } (-1)^ n x^ n, \, \, |x|<1 \]](images/img-0581.png)
integrando termo a termo, de
![\[ \dfrac {1}{1+x^2}=\sum _{n=0}^{\infty } (-1)^ n x^{2n}, \, \, |x|<1 \]](images/img-0582.png)
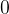 a
a  para
para  , temos
, temos
![\[ \operatorname{arctg}x=\sum _{n=0}^{\infty } (-1)^ n \dfrac {x^{2n+1}}{2n+1}, \, \, \, |x|\leq 1 \]](images/img-0584.png)
Example 76. Considere a série 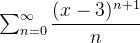 analisemos sobre o intervalo de convergência dessa série.
analisemos sobre o intervalo de convergência dessa série.
Solução: Usando o teste da razão
![\[ \lim _{n\to \infty } \left|\dfrac {(x-3)^{n+2}}{n+1}\dfrac {n}{(x-3)^{n+1}}\right|=\lim _{n\to \infty } |x-3|\dfrac {n}{n+1}=|x-3| \]](images/img-0586.png) |
essa série converge absolutamente se 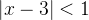 , que equivale a
, que equivale a 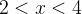 e diverge fora desse intervalo. No caso em que
e diverge fora desse intervalo. No caso em que 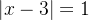 que corresponde a
que corresponde a 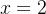 e
e 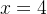 , quando substituimos
, quando substituimos 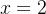 nessa série obtemos
nessa série obtemos 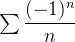 que converge e para
que converge e para 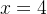 obtemos a série
obtemos a série 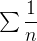 que diverge. Logo, o intervalo de convergência da série
que diverge. Logo, o intervalo de convergência da série 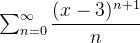 é o intervalo
é o intervalo