| Séries e Equações Diferenciais Ordinárias |
O polinômio de Taylor de uma função 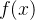 em torno de
em torno de  é
é
![\[ P_{n,a}(x)=f(a)+f’(a)(x-a)+\dfrac {f”(a)}{2!}(x-a)^2+\cdots +\dfrac {f^{(n)}(a)}{n!}(x-a)^ n=\sum _{k=0}^ n \dfrac {f^{(k)}(a)}{n!}(x-a)^ k \]](images/img-0620.png) |
O polinômio de Maclaurin de  é:
é:
![\[ P_ n(x)=f(0)+f’(0)x+\dfrac {f”(0)}{2!}x^2+\cdots +\dfrac {f^{(n)}(0)}{n!}x^ n=\sum _{k=0}^ n \dfrac {f^{(k)}(0)}{n!}x^ k \]](images/img-0621.png) |
que é o polinômio de Taylor de  em torno do ponto
em torno do ponto 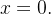 Por exemplo, o polinômio de Maclaurin de
Por exemplo, o polinômio de Maclaurin de 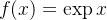 é
é
![\[ P_ n(x)=1+x+\dfrac {x^2}{2!}+\cdots +\dfrac {x^ n}{n!}. \]](images/img-0623.png) |
Theorem 79 (Fórmula de Taylor com resto). Seja 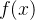 uma função de classe
uma função de classe 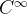 num intervalo que contém
num intervalo que contém 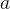 . Dado qualquer
. Dado qualquer  nesse intervalo existe um número real
nesse intervalo existe um número real 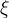 entre
entre 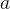 e
e  tal que
tal que
onde
![\[ f(x)=P_{n,a}(x)+R_ n (x) \]](images/img-0627.png)
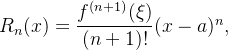 e
e
Além disso, a sequência
![\[ P_{n,a}(x)=f(a)+f’(a)(x-a)+\dfrac {f”(a)}{2!}(x-a)^2+\cdots +\dfrac {f^{(n)}(a)}{n!}(x-a)^ n \]](images/img-0629.png)
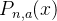 converge para
converge para 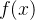 quando
quando 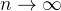 se, e somente se,
se, e somente se, 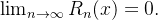
Considere a função ![$G:[a,x]\to \mathbb {R}$](images/img-0633.png) dada por
dada por
![\[ G(t)=f(x)-[f(t)+f’(t)(x-t)+\dfrac {f”(t)}{2!}(x-t)^2+\cdots +\dfrac {f^{(n)}(t)}{n!}(x-t)^ n]-R_ n(x)\dfrac {(x-t)^{n+1}}{(x-a)^{n+1}} \]](images/img-0634.png) |
com 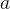 e
e  fixos, onde
fixos, onde 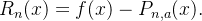 Observe que
Observe que  satisfaz as seguintes propriedades:
satisfaz as seguintes propriedades:
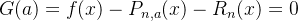
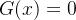
 é contínua no intervalo fechado
é contínua no intervalo fechado ![$[a,x]$](images/img-0639.png) e derivável no intervalo aberto
e derivável no intervalo aberto 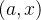 .
.
Logo, pelo teorema de Rolle existe um 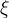 tal que
tal que 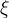 está entre
está entre 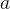 e
e  tal que
tal que 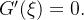 Mas
Mas
![\[ G’(t)=\dfrac {f^{(n+1)}(t)}{n!}(x-t)^ n-(n+1)R_ n(x)\dfrac {(x-t)^{n}}{(x-a)^{n+1}} \]](images/img-0642.png) |
e, portanto, 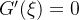 implica em
implica em 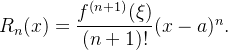
Note que a soma parcial de ordem 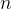 da série
da série 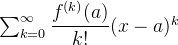 é
é 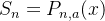 . Logo,
. Logo,
![\[ \lim _{n\to \infty } S_ n=\lim _{n\to \infty } P_{n,a}(x)=\lim _{n\to \infty }[f(x)-R_ n(x)]=f(x) \]](images/img-0647.png) |
Logo,
![\[ f(x)=\sum _{k=0}^{\infty } \dfrac {f^{(k)}(a)}{k!}(x-a)^ k. \]](images/img-0648.png) |
Example 80. Mostre que a série de potências 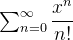 realmente representa a função
realmente representa a função 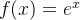 para todo
para todo  real.
real.
Solução: Ja vimos que  . Falta mostrar que esta série realmente representa a função exponencial
. Falta mostrar que esta série realmente representa a função exponencial 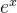 . Pela Fórmula de Taylor com resto, temos que
. Pela Fórmula de Taylor com resto, temos que
![\[ e^ x=P_ n(x)+R_ n(x) \]](images/img-0651.png) |
onde
![\[ P_ n(x)=1+x+\dfrac {x^2}{2!}+\cdots +\dfrac {x^ n}{n!} \]](images/img-0652.png) |
e
![\[ R_ n(x)=\dfrac {f^{(n+1)}(\xi )}{(n+1)!}(x)^{n+1}=\dfrac {e^{\xi }x^{n+1}}{(n+1)!} \]](images/img-0653.png) |
onde 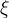 está entre
está entre  e
e  . Como
. Como 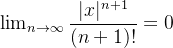 então
então
![\[ \lim _{n \to \infty } \left| \dfrac {e^{\xi }x^{n+1}}{(n+1)!} \right|=0. \]](images/img-0655.png) |
Logo, realmente a série representa a função 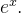
Example 81. Analise se a série da função 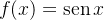 realmente a representa.
realmente a representa.
Solução: Temos que
![\[ f(0)=0, \, \, f’(0)=1, \, \, f”(0)=0, \, \, f”’(0)=-1, \cdots . \]](images/img-0657.png) |
Além disso,
![\[ f^{(n+1)}(\xi )=\begin{cases} \pm \operatorname{sen}\xi , \, \, n \, \, \mbox{par}\\ \pm \cos \xi , \, \, n \, \, \mbox{ímpar} \end{cases} \]](images/img-0658.png) |
e o resto
![\[ |R_ n(x)|=\left| \dfrac {f^{(n+1)} (\xi ) x^{n+1}}{(n+1)!}\right|\leq \dfrac {|x|^{n+1}}{(n+1)!} \]](images/img-0659.png) |
e, 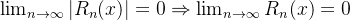 e portanto, a série do
e portanto, a série do  representa essa função.
representa essa função.
Remark 82. Uma função 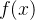 é analítica em
é analítica em  quando ela puder ser representada por sua série de Taylor em algum intervalo aberto em torno de
quando ela puder ser representada por sua série de Taylor em algum intervalo aberto em torno de 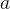 .
.
Um outro resultado que podemos deduzir da fórmula 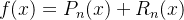 é que se aproximarmos o valor de
é que se aproximarmos o valor de 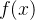 por
por 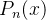 o erro que cometemos é da ordem de
o erro que cometemos é da ordem de 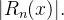
Example 83. Encontre o valor aproximado de 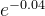 com erro menor que
com erro menor que 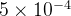 .
.
Solução: Temos que
![\[ e^ x=1+x+\dfrac {x^2}{2!}+\cdots +\dfrac {x^ n}{n!}+R_ n(x) \]](images/img-0667.png) |
se aproximarmos
![\[ e^{-0,04}\approx 1-0,04+\dfrac {(0,04)^2}{2!} \]](images/img-0668.png) |
então o erro que cometemos será de
![\[ |R_3 (-0,04)|\leq \dfrac {|(-0,04)^3}{3!}\approx \dfrac {0,000064}{3!}. \]](images/img-0669.png) |