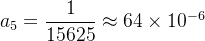2.3 Séries Alternadas
Séries do tipo 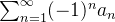 ou
ou 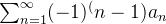 com os termos
com os termos  para todo
para todo 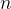 é dita série alternada. Ou seja,
é dita série alternada. Ou seja,
Theorem 53 (Critério de Leibniz). Seja 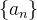 uma sequência de termos positivos com as propriedades:
uma sequência de termos positivos com as propriedades:
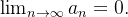
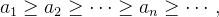 isto é,
isto é, 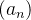 monótona decrescente.
monótona decrescente.
Então a série alternada 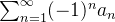 converge.
converge.
Considere a série alternada 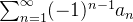 , temos que
, temos que
ou seja,
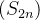
é monótona crescente, e reagrupando seus termos temos
logo,
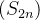
é limitada, segue que existe
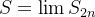
. Agora, como
passando o limite
logo, o
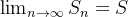
, portanto
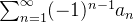
converge.
Example 54. A série 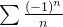 converge, pois o
converge, pois o 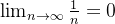 e
e 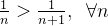 .
.
Example 55. A série 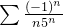 converge pelo teste de Leibniz.
converge pelo teste de Leibniz.
Example 56. A série 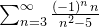 converge também pelo Teste de Leibniz.
converge também pelo Teste de Leibniz.
Theorem 57. O erro que se comete ao se aproximar a soma da série 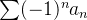 por
por 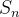 é de
é de 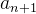 .
.
De fato,
Example 58. Para a série do exemplo 55 temos que o erro cometido para essa aproximação foi 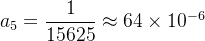
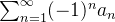 ou
ou 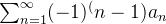 com os termos
com os termos  para todo
para todo 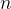 é dita série alternada. Ou seja,
é dita série alternada. Ou seja, ![\[ \sum _{n=1}^{\infty } (-1)^ n a_ n=-a_1+a_2+\cdots +(-1)^ n a_ n+ \cdots \]](images/img-0419.png)
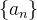 uma sequência de termos positivos com as propriedades:
uma sequência de termos positivos com as propriedades: 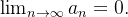
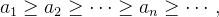 isto é,
isto é, 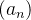 monótona decrescente.
monótona decrescente. 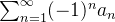 converge.
converge. 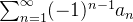 , temos que
, temos que ![\[ S_{2n}=(a_1-a_2)+(a_3-a_4)+\cdots +(a_{2n}-a_{2n-1}) \]](images/img-0423.png)
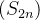 é monótona crescente, e reagrupando seus termos temos
é monótona crescente, e reagrupando seus termos temos ![\[ S_{2n}=a_1-(a_2-a_3)-(a_3-a_4)-\cdots -(a_{2n-1}-a_{2n})\leq a_1 \]](images/img-0425.png)
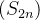 é limitada, segue que existe
é limitada, segue que existe 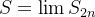 . Agora, como
. Agora, como ![\[ S_{2n+1}=S_{2n}+a_{2n+1} \]](images/img-0427.png)
![\[ \lim _{n\to \infty } S_{2n+1}=\lim _{n\to \infty } S_{2n}+ \lim _{n\to \infty } a_{2n+1}=S+0 \]](images/img-0428.png)
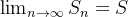 , portanto
, portanto 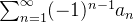 converge.
converge. 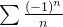 converge, pois o
converge, pois o 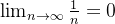 e
e 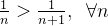 .
. 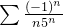 converge pelo teste de Leibniz.
converge pelo teste de Leibniz. 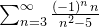 converge também pelo Teste de Leibniz.
converge também pelo Teste de Leibniz. 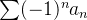 por
por 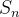 é de
é de 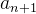 .
. ![\[ |S_ n -S|=|\sum _{k=n+1}^{\infty }(-1)^ k a_ k|=|(-1)^{n+1}a_{n+1}+(-1)^{n+2}a_{n+2}+\cdots | \]](images/img-0437.png)
![\[ =|(-1)^{n+1}[a_{n+1}-a_{n+2}+\cdots ]| \]](images/img-0438.png)
![\[ =a_{n+1}-a_{n+2}+a_{n+3}-a_{n+4}+\cdots \leq a_{n+1}. \]](images/img-0439.png)
![\[ S_4=-\dfrac {1}{5}+\dfrac {1}{50}-\dfrac {1}{325}+\dfrac {1}{2500}\approx -0,18 \]](images/img-0440.png)