2.4 Convergência Absoluta

Uma série 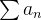$\sum a_ n$ converge absolutamente se a nova série 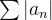$\sum |a_ n|$ converge. Por exemplo, a série 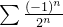$\sum \frac{(-1)^ n}{2^ n}$ converge absolutamente pois a série 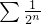$\sum \frac{1}{2^ n}$ é uma série geométrica de razão 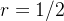$r=1/2$ e, portanto, convergente.

Theorem 59 (Convergência absoluta). Se uma série 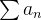$\sum a_ n$ é absolutamente convergente então ela é convergente.

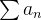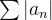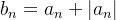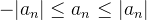Suponha que $\sum a_ n$ converge absolutamente então $\sum |a_ n|$ converge. Podemos considerar $b_ n=a_ n+|a_ n|$ como $-|a_ n|\leq a_ n \leq |a_ n|$ então

$0\leq b_ n\leq 2|a_ n|$

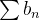Logo, $\sum b_ n$ converge pelo teste de comparação. Então

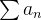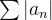$\sum a_ n=\sum (a_ n+|a_ n|)-|a_ n|$

converge. Uma série $\sum a_ n$ tal que $\sum |a_ n|$ diverge é dita condicionalmente convergente. Por exemplo, a série 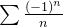$\sum \frac{(-1)^ n}{n}$ converge pelo teste das séries alternadas mas a série 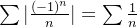$\sum |\frac{(-1)^ n}{n}|=\sum \frac{1}{n}$ diverge. Logo, a série 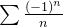$\sum \frac{(-1)^ n}{n}$ é condicionalmente convergente.

Example 60. A série 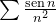$\sum \frac{\operatorname{sen}n}{n^2}$ converge ou diverge?

Solução: Note que

$|\operatorname{sen}n|\leq 1$

daí

$\frac{|\operatorname{sen}n|}{n^2}\leq \frac{1}{n^2}$

portanto 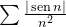$\sum \frac{|\operatorname{sen}n|}{n^2}$ converge, pelo teste de comparação, logo, a série 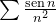$\sum \frac{\operatorname{sen}n}{n^2}$ converge absolutamente.