| Séries e Equações Diferenciais Ordinárias |
Uma série  é uma série de termos positivos se
é uma série de termos positivos se  para todo
para todo 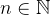 . Note que quando
. Note que quando  é uma série de termos positivos então a sequência de somas parciais
é uma série de termos positivos então a sequência de somas parciais 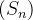 dessa série é crescente, isto é,
dessa série é crescente, isto é,
![\[ S_1\leq S_2 \leq \cdots \leq S_ n \leq \cdots \]](images/img-0342.png) |
logo, para que a série  convirja bast mostrar que
convirja bast mostrar que 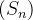 é limitada.
é limitada.
Theorem 42 (Teste de comparação). Sejam se se  e
e 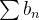 séries de termos positivos. Temos que:
séries de termos positivos. Temos que:
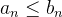 , para todo
, para todo 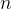 e se
e se 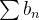 converge então
converge então  converge.
converge. 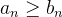 , para todo
, para todo 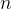 e se
e se 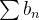 diverge então
diverge então  diverge.
diverge.
Suponha que  e
e 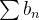 sejam séries de termos positivos, com
sejam séries de termos positivos, com 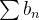 convergente e suponha que
convergente e suponha que
![\[ a_ n\leq b_ n, \, \, \, \forall n\in \mathbb {N} \]](images/img-0345.png) |
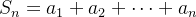 e
e 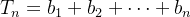 então
então ![\[ S_ n\leq T_ n \]](images/img-0348.png) |
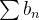 converge então
converge então 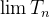 existe. Logo
existe. Logo 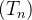 é limitada, desse modo, existe
é limitada, desse modo, existe 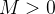 tal que
tal que 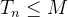 . Assim,
. Assim, ![\[ S_ n\leq M, \, \, \, \, \forall n \]](images/img-0351.png) |
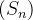 é convergente, logo
é convergente, logo  converge. Por outro lado, se
converge. Por outro lado, se 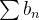 diverge e
diverge e 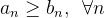 , então
, então ![\[ S_ n\geq T_ n, \, \, \, \forall n \]](images/img-0353.png) |
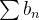 diverge então
diverge então 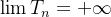 . Desse modo,
. Desse modo, 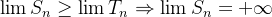 o que implica
o que implica  diverge.
diverge. Example 43. Mostre que a série 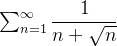 diverge.
diverge.
De fato, note que
![\[ n+\sqrt{n}<2n \Rightarrow \dfrac {1}{n+\sqrt{n}}>\dfrac {1}{2n} \]](images/img-0357.png) |
como 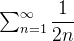 diverge então pelo teste de comparação segue que
diverge então pelo teste de comparação segue que 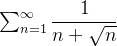 também diverge.
também diverge.
Example 44. Analise sobre a convergência ou divergência da série 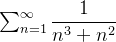 .
.
Solução: Note que 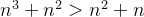 o que implica em
o que implica em
![\[ \dfrac {1}{n^3+n^2}<\dfrac {1}{n^2+n}, \, \, \, \forall n \]](images/img-0361.png) |
como 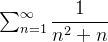 converge então pelo teste de comparação a série
converge então pelo teste de comparação a série 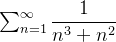 converge.
converge.
Theorem 45 (Teste da Integral). Seja a série a série 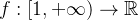 contínua e suponhamos que
contínua e suponhamos que  é positiva e decrescente então:
é positiva e decrescente então:
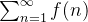 é convergente se
é convergente se 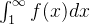 for convergente,
for convergente, 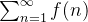 é divergente se
é divergente se 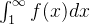 for divergente.
for divergente.
Seja 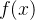 função monótona decrescente e positiva. Temos que
função monótona decrescente e positiva. Temos que
![\[ f(2)+f(3)+\cdots +f(n)\leq \int _1^ n f(x)dx\leq f(1)+f(2)+\cdots +f(n-1) \]](images/img-0365.png) |
![\[ S_ n\leq f(1)+\int _1^ n f(x)dx \]](images/img-0366.png) |
![\[ S_ n\leq f(1)+\int _1^ n f(x)dx\leq f(1)+\int _1^{\infty } f(x)dx \]](images/img-0367.png) |
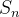 é limitada então
é limitada então 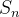 é convergente, portanto,
é convergente, portanto, 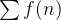 converge. De modo análogo,como
converge. De modo análogo,como ![\[ \int _1^ n f(x)dx \leq S_{n-1} \]](images/img-0370.png) |
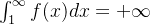 então
então 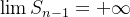 , logo,
, logo, 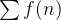 diverge.
diverge. Example 46. Seja Tomando
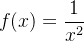 temos que
temos que 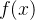 é positiva e decrescente já que
é positiva e decrescente já que 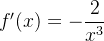 . A integral
. A integral 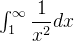 converge e, portanto,
converge e, portanto, 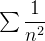 converge.
converge. 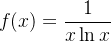 atende às condições expostas mas
atende às condições expostas mas ![$\int _2^{\infty } \dfrac {1}{x \ln x}=\lim _{B\to \infty } [\ln (\ln x))]_2^ B=+\infty $](images/img-0378.png) , logo
, logo 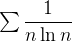 diverge.
diverge. 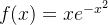 ,
, 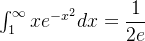 o que implica
o que implica 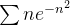 converge.
converge.
A série 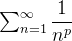 é uma p-série. Analisemos sobre a convergência ou divergência dessa série. Temos o seguinte resultado.
é uma p-série. Analisemos sobre a convergência ou divergência dessa série. Temos o seguinte resultado.
Theorem 47. A p-série 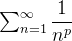 converge se
converge se 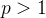 e diverge se
e diverge se 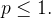
Calculemos a integral,
![\[ \int _1^{\infty } \dfrac {1}{x^ p}dx=\lim _{B\to \infty } \int _1^ B \dfrac {1}{x^ p}dx=\lim _{B\to \infty } [B^{1-p} -1], \, \, p\neq 1 \]](images/img-0386.png) |
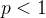 , temos que o
, temos que o 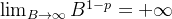 , se
, se 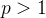 então
então 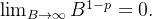
Theorem 48 (Forma limite do teste de comparação). Sejam se se se  e
e 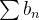 duas séries de termos positivos e seja
duas séries de termos positivos e seja 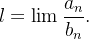
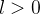 então ou ambas as séries
então ou ambas as séries 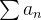 e
e 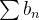 convergem ou ambas divergem
convergem ou ambas divergem 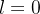 e
e 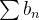 converge então
converge então  converge.
converge. 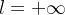 e
e 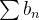 diverge então
diverge então  diverge.
diverge.
Fixado 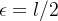 podemos encontrar
podemos encontrar 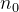 tal que
tal que
![\[ \dfrac {l}{2}b_ n \leq a_ n \leq \dfrac {3}{2}lb_ n, \forall n\geq n_0 \]](images/img-0395.png) |
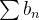 converge então
converge então 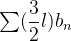 também converge e como
também converge e como 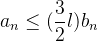 para todo
para todo 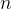 segue o resultado. Por outro lado, se
segue o resultado. Por outro lado, se 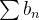 diverge como
diverge como 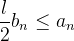 para todo
para todo 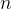 , segue que
, segue que  diverge, já que
diverge, já que 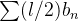 diverge.
diverge. Example 49. Considere a série 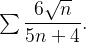 Ela converge ou diverge?
Ela converge ou diverge?
Solução: Para encontrar uma série que possamos comparar com a série dada olhamos os termos que dominam no numerador e denominador da série original, neste caso, escolhemos 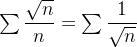 para comparar com a série dada, já sabemos que a série
para comparar com a série dada, já sabemos que a série 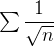 é uma p-série com
é uma p-série com 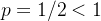 logo, diverge. E como
logo, diverge. E como 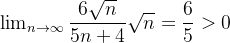 então pela forma limite do teste de comparação segue que
então pela forma limite do teste de comparação segue que 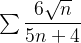 diverge.
diverge.
Example 50. As séries 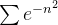 e
e 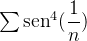 convergem ou divergem?
convergem ou divergem?
Solução: Como 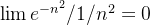 e
e 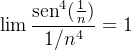 então ambas as séries convergem, pela forma limite do teste de comparação, já que as séries
então ambas as séries convergem, pela forma limite do teste de comparação, já que as séries 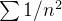 e
e 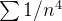 convergem.
convergem.
Theorem 51 (Reagrupamento). O reagrupamento de séries de termos positivos que sejam convergentes não altera a convergência da série.
Dadas duas séries  e
e 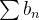 convergentes então
convergentes então 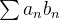 não é necessariamente convergente. Além disso,
não é necessariamente convergente. Além disso,
![\[ \sum a_ n b_ n \neq \sum a_ n \sum b_ n=\sum c_ n \]](images/img-0413.png) |
onde
![\[ \sum _{n=0}^{\infty } c_ n=\sum _{n=0}^{\infty } \sum _{j=0}^ n a_ j b_{n-j} \]](images/img-0414.png) |
Example 52. Temos que a série 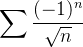 converge mas
converge mas 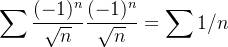 diverge.
diverge.