2.1.1 A série harmônica

A série harmônica é série 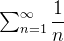$\sum _{n=1}^{\infty } \dfrac {1}{n}$ . Temos que

$S_ n=1+\dfrac {1}{2}+\dfrac {1}{3}+\cdots +\dfrac {1}{n}$

$S_{2n}=1+\dfrac {1}{2}+\dfrac {1}{3}+\cdots +\dfrac {1}{n}+\dfrac {1}{n+1}+\cdots +\dfrac {1}{2n}$

Logo,

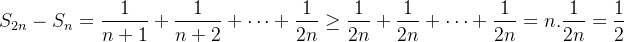$\begin{equation} S_{2n}-S_ n=\dfrac {1}{n+1}+\dfrac {1}{n+2}+\cdots +\dfrac {1}{2n}\geq \dfrac {1}{2n}+\dfrac {1}{2n}+\cdots +\dfrac {1}{2n}=n.\dfrac {1}{2n}=\dfrac {1}{2}\label{desig} \end{equation}$

(2.1)

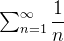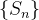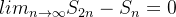se a série $\sum _{n=1}^{\infty } \dfrac {1}{n}$ fosse convergente então as sequências de somas parciais $\{ S_ n\}$ e $\{ S_{2n}\}$ convergiriam e teriam o mesmo limite, e dessa forma, $lim_{n\to \infty } S_{2n}-S_ n=0$ Mas, isto é impossível, pois a desigualdade em (2.1) implica em 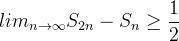$lim_{n\to \infty } S_{2n}-S_ n\geq \dfrac {1}{2}$ . Logo, 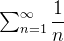$\sum _{n=1}^{\infty } \dfrac {1}{n}$ diverge.

O acréscimo ou omissão de um número finito de termos não altera a convergência ou divergência de uma série. Podemos daí deduzir que uma série 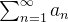$\sum _{n=1}^{\infty } a_ n$ converge se, e somente se, 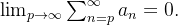$\lim _{p\to \infty } \sum _{n=p}^{\infty } a_ n=0.$ Esse é o critério de Cauchy dado abaixo.

Theorem 38 (Critério de Cauchy). Uma série $\sum a_ n$ converge se, e somente se, dado 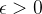$\epsilon >0$ existe 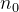$n_0$ tal que

$|S_ n-S_ m|< \epsilon , \, \, \forall n>m\geq n_0.$

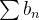Theorem 39. Se as séries $\sum a_ n$ e $\sum b_ n$ diferem apenas em uma quantidade finita de termos então ou ambas convergem ou ambas divergem.

Por hipótese, existe um índice 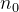$n_0$ tal que 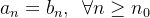$a_ n=b_ n, \, \, \, \forall n\geq n_0$ . Logo:

$S_ n=a_1+\cdots +a_{n_0}+b_{n_0+1}+\cdots +b_ n$

$T_ n=b_1+\cdots +b_{n_0}+b_{n_0+1}+\cdots +b_ n$

daí

$S_ n=S_{n_0}-T_{n_0}+T_ n$

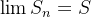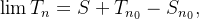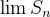e $\lim S_ n=S$ então $\lim T_ n=S+T_{n_0}-S_{n_0},$ e se $\lim S_ n$ não existe então 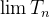$\lim T_ n$ também não existe.

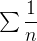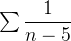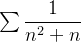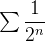Example 40. As séries $\sum \dfrac {1}{n}$ e $\sum \dfrac {1}{n-5}$ são divergentes e as séries $\sum \dfrac {1}{n^2+n}$ e $\sum \dfrac {1}{2^ n}$ são convergentes.

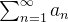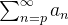Como consequência do Teorema 39 as séries $\sum _{n=1}^{\infty } a_ n$ e $\sum _{n=p}^{\infty } a_ n$ são ambas convergentes ou ambas divergentes.

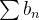Theorem 41 (Propriedades das séries). Sejam $\sum a_ n$ e $\sum b_ n$ séries numéricas e seja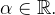 $\alpha \in \mathbb {R}.$

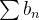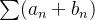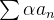Se $\sum a_ n$ e $\sum b_ n$ convergem então $\sum (a_ n+b_ n)$ convergem e $\sum \alpha a_ n$ convergem.
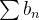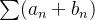Se $\sum a_ n$ converge e $\sum b_ n$ diverge então $\sum (a_ n+b_ n)$ diverge.
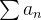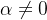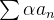Se $\sum a_ n$ diverge e $\alpha \neq 0$ então $\sum \alpha a_ n$ diverge.

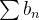Se $\sum a_ n$ e $\sum b_ n$ divergem nada podemos afirmar sobre 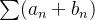$\sum (a_ n+b_ n)$ . Tal soma pode convergir ou não. Exemplo, 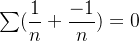$\sum (\dfrac {1}{n}+\dfrac {-1}{n})=0$ converge, mas 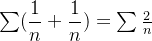$\sum (\dfrac {1}{n}+\dfrac {1}{n})=\sum \frac{2}{n}$ diverge.