2.1 Séries Numéricas

Dada uma sequência 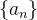$\{ a_ n\}$ de números reais, a soma infinita

$a_1+a_2+a_3+\cdots +a_ n+\cdots$

será representada por 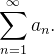$\displaystyle \sum _{n=1}^{\infty } a_ n.$ Tais somas infinitas são chamadas de séries infinitas ou, simplesmente, séries.

Example 33.

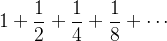A soma $1+\dfrac {1}{2}+\dfrac {1}{4}+\dfrac {1}{8}+\cdots$ que é representada por 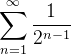$\displaystyle \sum _{n=1}^{\infty } \dfrac {1}{2^{n-1}}$ é uma série geométrica.
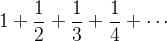A soma infinita $1+\dfrac {1}{2}+\dfrac {1}{3}+\dfrac {1}{4}+\cdots$ representamos por 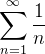$\displaystyle \sum _{n=1}^{\infty } \dfrac {1}{n}$ é conhecida como a série harmônica.

Dada uma série infinita 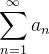$\displaystyle \sum _{n=1}^{\infty } a_ n$ , as somas parciais dessa série são:

$S_1=a_1, \quad S_2=a_1+a_2, \quad S_3=a_1+a_2+a_3,\quad \cdots ,\quad S_ n=a_1+a_2+\cdots +a_ n$

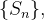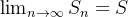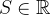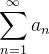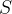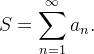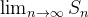Formamos então uma sequência de somas parciais $\{ S_ n\} ,$ se $\lim _{n \to \infty } S_ n=S$ , $S\in \mathbb {R}$ então dizemos que a série $\displaystyle \sum _{n=1}^{\infty } a_ n$ converge e sua soma é $S$ , isto é, $S=\displaystyle \sum _{n=1}^{\infty } a_ n.$ Se $\lim _{n \to \infty } S_ n$ não existe então dizemos que a série 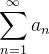$\displaystyle \sum _{n=1}^{\infty } a_ n$ diverge.

Example 34. Seja 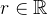$r\in \mathbb {R}$ e considere a série 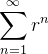$\displaystyle \sum _{n=1}^{\infty } r^ n$ , vamos analisar sobre a convergência ou divergência dessa série.

Seja 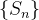$\{ S_ n\}$ a sequência de somas parciais de ordem 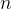$n$ da série 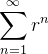$\displaystyle \sum _{n=1}^{\infty } r^ n$ , isto é,

$S_ n=1+r+r^2+\cdots +r^ n$

temos que

$rS_ n=r+r^2+\cdots +r^ n+r^{n+1}$

daí

$(1-r)S_ n=1-r^{n+1}$

$S_ n=\dfrac {1-r^{n+1}}{1-r}$

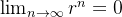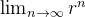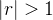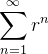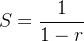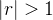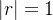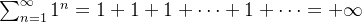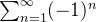como $\lim _{n\to \infty } r^ n=0$ se $|r|<1$ e $\lim _{n\to \infty } r^ n$ não existe se $|r|>1$ , então concluímos que a série $\displaystyle \sum _{n=1}^{\infty } r^ n$ converge e sua soma é $S=\dfrac {1}{1-r}$ se $|r|<1$ e, diverge se $|r|>1$ . No caso em que $|r|=1$ a essa série também diverge, pois $\sum _{n=1}^{\infty }1^ n=1+1+1+\cdots +1+\cdots =+\infty$ e $\sum _{n=1}^{\infty }(-1)^ n$ não existe. 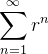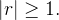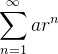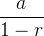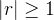Conclusão a série $\displaystyle \sum _{n=1}^{\infty } r^ n$ converge se $|r|<1$ e diverge se $|r|\geq 1.$ De forma análoga, a série $\displaystyle \sum _{n=1}^{\infty } ar^ n$ converge para $\dfrac {a}{1-r}$ se $|r|<1$ e diverge se $|r|\geq 1$ , tal série é chamada de série geométrica.

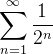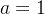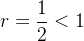Example 35. A série $\displaystyle \sum _{n=1}^{\infty } \dfrac {1}{2^ n}$ é uma série geométrica com $a=1$ e $r=\dfrac {1}{2}<1$ , portanto converge e sua soma é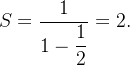 $S=\dfrac {1}{1-\dfrac {1}{2}}=2.$

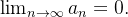
Theorem 36 (Teste do n-ésimo termo). Se uma série $\sum a_ n$ converge então $\lim _{n \to \infty } a_ n=0.$

Temos que

$a_ n=S_ n-S_{n-1}$

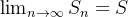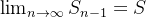como $\sum a_ n$ converge então $\lim _{n \to \infty } S_ n=S$ e $\lim _{n \to \infty } S_{n-1}=S$ daí

$\lim _{n\to \infty } a_ n=\lim _{n\to \infty } S_ n-\lim _{n \to \infty } S_{n-1}=S-S=0.$

Example 37.

A série 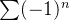$\sum (-1)^ n$ diverge pois 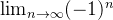$\lim _{n\to \infty } (-1)^ n$ não existe, logo, pelo teste do n-ésimo termo a série 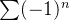$\sum (-1)^ n$ não pode convergir.
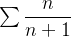A série $\sum \dfrac {n}{n+1}$ diverge, pois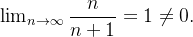 $\lim _{n\to \infty } \dfrac {n}{n+1}=1\neq 0.$

Consideremos a série 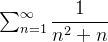$\sum _{n=1}^{\infty } \dfrac {1}{n^2+n}$ . Note que, 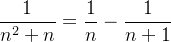$\dfrac {1}{n^2+n}=\dfrac {1}{n}-\dfrac {1}{n+1}$ e

$S_ n=1-\dfrac {1}{2}+\dfrac {1}{2}-\dfrac {1}{3}+\dfrac {1}{3}+\cdots +\dfrac {1}{n}-\dfrac {1}{n+1}=1-\dfrac {1}{n+1}$

Logo,

$\lim _{n\to \infty } S_ n =1-\lim _{n \to \infty } \dfrac {1}{n+1}=1$

portanto, 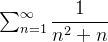$\sum _{n=1}^{\infty } \dfrac {1}{n^2+n}$ converge para 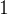$1$ . Tal série é conhecida como séries de termos encaixantes. De um modo geral, a série de termos encaixantes pode ser dada por

$\sum _{n=1}^{\infty } (b_ n-b_{n+1})$

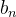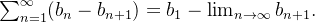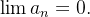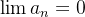se $b_ n$ convergir então $\sum _{n=1}^{\infty } (b_ n-b_{n+1})=b_1-\lim _{n\to \infty } b_{n+1}.$ Note que se uma série $\sum a_ n$ converge então necessariamente $\lim a_ n=0.$ Mas se $\lim a_ n=0$ não implica que 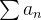$\sum a_ n$ convirja.

Um exemplo de série que satisfaz o fato de 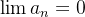$\lim a_ n=0$ mas que ela diverge é a série harmônica que será estudada na próxima subseção.