| Séries e Equações Diferenciais Ordinárias |
Definition 14. Dizemos que 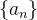 converge para um número real
converge para um número real 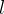 se dado
se dado 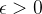 , existe
, existe 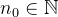 tal que
tal que 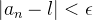 , para todo
, para todo 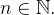 Neste caso, denotamos
Neste caso, denotamos 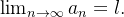 E dizemos que
E dizemos que 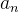 é convergente. Caso contrário, se tal limite não existe, dizemos que a sequência
é convergente. Caso contrário, se tal limite não existe, dizemos que a sequência 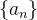 é divergente.
é divergente.
Note que;
![\[ |a_ n-l|<\epsilon \]](images/img-0086.png) |
se, e somente se,
![\[ -\epsilon <a_ n-l<\epsilon \]](images/img-0087.png) |
ou,
![\[ l-\epsilon <a_ n<l+\epsilon \]](images/img-0088.png) |
isto é,
![\[ a_ n \in (l-\epsilon ,l+\epsilon ). \]](images/img-0089.png) |
Um número finito de termos não altera a convergência nem a divergência de uma sequência.
Theorem 15. Uma sequência convergente 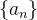 não pode ter dois limites.
não pode ter dois limites.
De fato, se supomos que 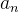 converge e
converge e 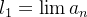 e
e 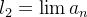 com
com 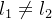 então (suponha
então (suponha 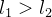 )
)
![\[ l_1-l_2=|l1-l2|=|l_1-a_ n+a_ n+l_2|\leq |l_1-a_ n|+|a_ n-l_2|<2\epsilon \]](images/img-0094.png) |
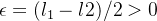 , desse modo, obtemos,
, desse modo, obtemos, 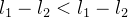 o que é absurdo.
o que é absurdo. Example 16. Vamos mostrar que Consideremos a sequência Escolhendo o primeiro A sequência Escolha Existem sequências (não limitadas) cujos termos crescem indefinidamente à medida que Se Se
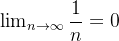 . Dado
. Dado 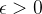 ,
, 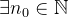 tal que
tal que 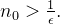 Logo, se
Logo, se  então
então 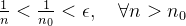 e assim
e assim 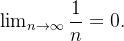
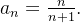 Neste caso,
Neste caso, 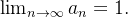 Dado
Dado 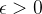 , note que
, note que
![\[ |\frac{n}{n+1}-1|<\epsilon \Leftrightarrow \frac{1}{n+1}<\epsilon \Leftrightarrow n>\frac{1}{\epsilon }-1 \]](images/img-0105.png)
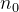 tal que
tal que 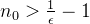 então para todo
então para todo  temos
temos
![\[ n>\frac{1}{\epsilon }-1 \Rightarrow \frac{1}{n+1}<\epsilon \Rightarrow |\frac{n}{n+1}-1|<\epsilon . \]](images/img-0107.png)
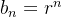 , onde
, onde 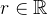 , fixo, tal que
, fixo, tal que 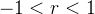 , converge para zero. Escolha
, converge para zero. Escolha 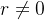 , dado
, dado 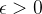 , como
, como 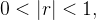 temos que
temos que 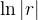 está definido, é diferente de zero, e
está definido, é diferente de zero, e 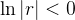 . Assim
. Assim
![\[ |r^ n-0|=|r|^ n <\epsilon \Leftrightarrow n \ln |r|< \ln \epsilon \Leftrightarrow n>\dfrac {\ln \epsilon }{\ln |r|} \]](images/img-0115.png)
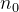 maior ou igual a
maior ou igual a 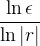 assim
assim  o que implica em
o que implica em 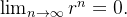
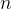 aumenta, por exemplo, a sequência
aumenta, por exemplo, a sequência 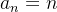 . Nesse caso, dizemos que a sequência tem limite infinito e denotamos
. Nesse caso, dizemos que a sequência tem limite infinito e denotamos 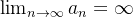 , isso significa que dado
, isso significa que dado 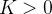 qualquer, existe
qualquer, existe 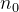 tal que
tal que 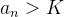 para todo
para todo 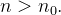 Para a sequência
Para a sequência 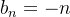 ,
, 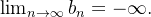
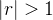 então
então 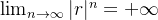 e
e 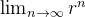 não existe.
não existe. 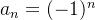 e como,
e como, 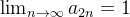 e
e 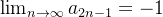 , logo, o limite de
, logo, o limite de 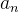 não existe.
não existe.
Theorem 17. Toda sequência convergente é limitada.
Seja 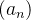 uma sequência convergente com limite
uma sequência convergente com limite 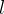 . Isto é,
. Isto é, 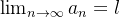 ou dado
ou dado 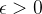 ,
, 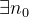 tal que
tal que 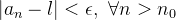 ou seja,
ou seja,
![\[ -\epsilon <a_ n-l<\epsilon , \, \, \forall n>n_0 \]](images/img-0134.png) |
![\[ |a_ n|<|l|+\epsilon , \, \, \, \forall n>n_0 \]](images/img-0135.png) |
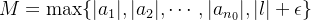 então
então ![\[ |a_ n|\leq M, \, \, \, \forall n\in \mathbb {N} \]](images/img-0137.png) |
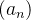 é limitada. A recíproca não é verdadeira pois, por exemplo, a sequência
é limitada. A recíproca não é verdadeira pois, por exemplo, a sequência 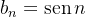 é limitada mas
é limitada mas 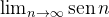 não existe.
não existe. Theorem 18. Sejam 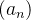 uma sequência limitada e
uma sequência limitada e 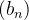 uma sequência que converge a zero então
uma sequência que converge a zero então 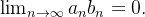
Como 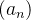 é limitada então existe
é limitada então existe 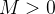 tal que
tal que 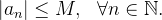 Por outro lado, como
Por outro lado, como 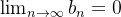 então dado
então dado 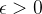 , existe
, existe 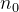 tal que
tal que 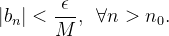 Desse modo,
Desse modo,
![\[ |a_ n b_ n|=|a_ n||b_ n|\leq M \frac{\epsilon }{M}<\epsilon , \, \, \forall n>n_0 \]](images/img-0146.png) |
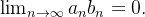
Example 19. A sequência 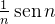 converge a zero. Pois,
converge a zero. Pois, 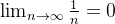 e
e 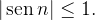 E pelo teorema 18 temos que
E pelo teorema 18 temos que 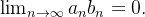
Theorem 20. Temos que o 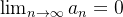 se, e somente se,
se, e somente se, 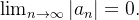
Note que se 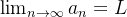 então necessariamente, o
então necessariamente, o 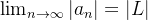 . (Isso porque
. (Isso porque 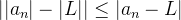 ). Mas, se
). Mas, se 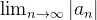 existe isso não implica que
existe isso não implica que 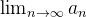 exista. Pois,
exista. Pois, 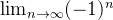 não existe, mas
não existe, mas 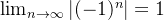 .
.
Theorem 21. Se 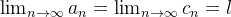 e
e 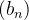 é tal que
é tal que 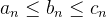 então
então 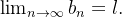
De fato, 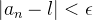 e
e 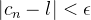 então
então
![\[ l-\epsilon <a_ n<l+\epsilon , \, \, \forall n>n_1 \]](images/img-0163.png) |
![\[ l-\epsilon <c_ n<l+\epsilon \, \, \forall n>n_2 \]](images/img-0164.png) |
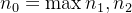 então
então ![\[ l-\epsilon <a_ n\leq b_ n\leq c_ n<l+\epsilon , \, \, \forall n>n_0 \]](images/img-0166.png) |
![\[ l-\epsilon <b_ n<l+\epsilon , \, \, \forall n>n_0 \]](images/img-0167.png) |
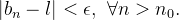
Theorem 22. Se 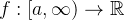 é uma função tal que
é uma função tal que 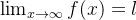 , então a sequência
, então a sequência 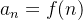 ,
, 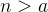 é convergente e
é convergente e 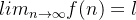 . Se
. Se 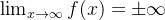 então
então 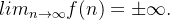
Example 23. Considere a sequência 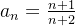 e calcule o
e calcule o 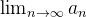 .
.
Note que a função 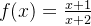 é tal que
é tal que 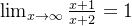 então
então 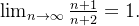
Example 24. Para calcular o 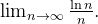 Tomamos a função
Tomamos a função 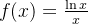 e como
e como
segue que
![\[ \lim _{x\to \infty } \frac{\ln x}{x}=\lim _{x\to \infty } \frac{1}{x}=0 \]](images/img-0182.png)