| Séries e Equações Diferenciais Ordinárias |
Definition 9. Uma sequência 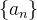 é dita crescente ou não decrescente quando
é dita crescente ou não decrescente quando 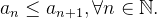 Se
Se 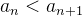 ela é dita estritamente crescente.
ela é dita estritamente crescente.
Definition 10. Uma sequência 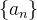 é dita decrescente ou não crescente quando
é dita decrescente ou não crescente quando 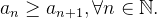 Se
Se 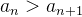 ela é dita estritamente decrescente.
ela é dita estritamente decrescente.
Definition 11. Uma sequência é dita monótona se ela é crescente ou decrescente.
Example 12. As sequências A sequência A sequência
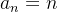 e
e 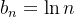 são crescentes, enquanto que,
são crescentes, enquanto que, 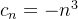 e
e 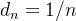 são decrescentes.
são decrescentes. 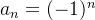 não é monótona, isto é, ela não é crescente nem decrescente. É uma sequência alternada.
não é monótona, isto é, ela não é crescente nem decrescente. É uma sequência alternada. 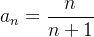 é crescente. De fato, note que
é crescente. De fato, note que
![\[ \dfrac {a_{n+1}}{a_ n}=\dfrac {n+1}{n+2}\dfrac {n+1}{n}=\dfrac {n^2+2n+1}{n^2+2n}\geq 1, \forall n. \]](images/img-0074.png)
A monotonicidade de alguma sequências pode ser deduzida por investigação do sinal da derivada da função extensão. Isto é, se 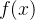 satisfaz
satisfaz 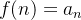 . Por exemplo, para a sequência,
. Por exemplo, para a sequência, 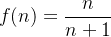 , podemos analisar a função
, podemos analisar a função 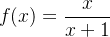 e como,
e como, 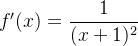 que é positiva, logo,
que é positiva, logo, 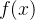 é crescente e, por sua vez,
é crescente e, por sua vez, 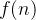 também é crescente.
também é crescente.
Example 13. Para a sequência 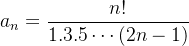 não é possível definir a função extensão. Mas note que,
não é possível definir a função extensão. Mas note que,
logo,
![\[ \dfrac {a_{n+1}}{a_ n}=\dfrac {1.3.5\cdots (2n-1)}{1.3.5\cdots (2n-1)(2n+1)}\dfrac {(n+1)!}{n!}=\dfrac {n+1}{2n+1}<1 \]](images/img-0080.png)
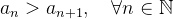 o que implica que
o que implica que 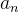 é decrescente.
é decrescente.