| Séries e Equações Diferenciais Ordinárias |
Sejam 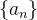 e
e 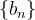 sequências convergentes limites
sequências convergentes limites 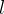 e
e  , respectivamente. Então:
, respectivamente. Então:
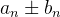 converge para
converge para 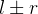 ;
;
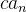 converge para
converge para 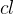 ;
;
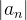 converge para
converge para 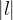 ;
;
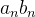 converge para
converge para 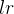 ;
;
se 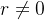 então
então 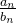 converge para
converge para 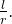
Vamos provar uma das propriedades acima, por exemplo, pode ser a propriedade 4. Suponha que 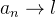 e
e 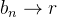 então dado
então dado 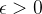 , existe
, existe 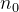 tal que
tal que 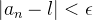 e
e 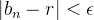 para todo
para todo 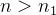 e
e  , assim, se
, assim, se 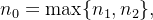 temos que para
temos que para 
![\[ |a_ n b_ n-lr|<|a_ n b_ n -a_ nr+a_ nr-lr|\leq |a_ n||b_ n-r|+|r||a_ n-l|<M\epsilon +|r|\epsilon =(M+|r|)\epsilon . \]](images/img-0202.png) |
Example 25. Analise sobre a convergência das sequências a seguir:
![\[ (a) \, \, a_ n=\frac{3n+1}{5n}+\frac{(-1)}{n} \quad (b)\, \, b_ n=\cos \frac{1}{n}(1+\frac{1}{n})\quad (c)\, \, c_ n=\frac{n^2+3}{4n^2-2n+1}. \]](images/img-0203.png)
Theorem 26. Toda sequência monótona limitada é convergente.
Suponha 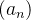 uma sequência crescente e limitada. Segue que existe
uma sequência crescente e limitada. Segue que existe 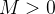 tal que
tal que
![\[ |a_ n|\leq M, \, \, \, \forall n \]](images/img-0204.png) |
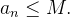 Logo,
Logo, 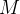 é uma cota superior para
é uma cota superior para 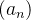 , seja
, seja 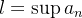 então
então 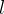 é a menor das cotas superiores de
é a menor das cotas superiores de 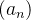 , assim
, assim  não é cota superior de
não é cota superior de 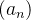 então existe
então existe 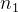 tal que
tal que ![\[ l-\epsilon <a_{n_1}\leq l. \]](images/img-0209.png) |
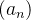 é crescente então
é crescente então 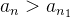 para todo
para todo 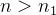 , segue que,
, segue que, ![\[ l-\epsilon <a_ n<l+\epsilon , \, \, \, \forall n>n_1 \]](images/img-0211.png) |
![\[ |a_ n-l|<\epsilon , \, \, \, \forall n>n_1 \]](images/img-0212.png) |
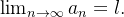
Example 27. Vimos que a sequência cujo termo geral é 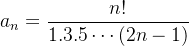 é decrescente. Veriquemos que ela também é limitada.
é decrescente. Veriquemos que ela também é limitada.
De fato, temos que
![\[ 0<a_ n=\dfrac {1}{1}\dfrac {2}{3}\dfrac {3}{5}\cdots \dfrac {n}{2n-1}\leq 1.1.1\cdots 1=1,\, \, \, \forall n \]](images/img-0213.png) |
Logo, pelo teorema 26 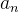 é convergente. Além disso,
é convergente. Além disso, 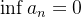 . Logo,
. Logo, 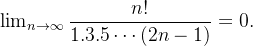
Theorem 28. Se uma sequência 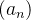 converge para um
converge para um 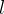 então todas as subsequências dela convergem para
então todas as subsequências dela convergem para 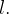
Se pelo menos uma das subsequências de 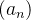 digamos
digamos 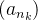 tivesse um outro limite
tivesse um outro limite 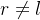 então
então 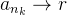 e
e 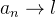 com
com 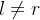 , mas isto contradiz o fato de limite ser único.
, mas isto contradiz o fato de limite ser único.
Example 29. A sequência 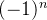 possui subsequências tais que
possui subsequências tais que 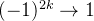 e
e 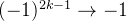 . Logo,
. Logo, 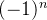 não converge. Por outro lado, a sequência
não converge. Por outro lado, a sequência 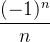 converge para zero, pois
converge para zero, pois 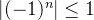 e
e 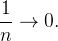 Assim,
Assim, 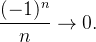
Theorem 30. Teste da Razão para sequências Se uma sequência 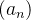 de termos positivos satisfaz à condição
de termos positivos satisfaz à condição 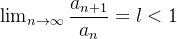 então ela converge para zero.
então ela converge para zero.
Seja 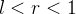 tal que
tal que 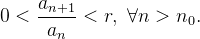 Como
Como 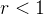 então
então 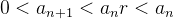 o que implica em
o que implica em 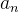 ser decrescente para
ser decrescente para  Assim
Assim 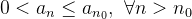 o que implica em
o que implica em 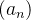 ser limitada. Logo,
ser limitada. Logo, 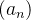 é convergente. Suponha, por absurdo, que
é convergente. Suponha, por absurdo, que 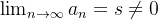 então
então
![\[ l=\lim _{n\to \infty }\dfrac {a_{n+1}}{a_ n}=\dfrac {\lim a_{n+1}}{\lim a_ n}=\dfrac {s}{s}=1. \]](images/img-0236.png) |
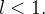
Example 31. As sequências 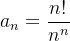 ,
, 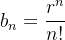 ,
, 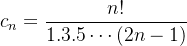 ,
, 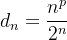 convergem todas a zero.
convergem todas a zero.
De fato, para a sequência 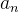 temos
temos
![\[ \lim _{n\to \infty } \dfrac {a_{n+1}}{a_ n}=\lim _{n\to \infty } \dfrac {(n+1)!}{(n+1)^(n+1)}\dfrac {n^ n}{n!}=\lim _{n\to \infty }(\dfrac {n}{n+1)})^ n=\dfrac {1}{e}<1 \]](images/img-0242.png) |
aqui usou-se o limite fundamental:
![\[ \lim _{x\to \infty }(1+\dfrac {1}{x})^ x=e \]](images/img-0243.png) |
Para a sequência 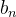 temos
temos
![\[ \lim _{n\to \infty } \dfrac {b_{n+1}}{b_ n}=\lim _{n\to \infty } \dfrac {r^(n+1)}{(n+1)!}\dfrac {n!}{r^ n}=\lim _{n\to \infty } \dfrac {r}{n+1}=0, \]](images/img-0245.png) |
e, para a sequência 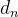 temos
temos
![\[ \lim _{n\to \infty } \dfrac {d_{n+1}}{d_ n}=\lim {n \to \infty } \dfrac {(n+1)^ p}{2^(n+1)}\dfrac {2^ n}{n^ p}=\dfrac {1}{2}\lim _{n \to \infty } (\dfrac {n+1}{n})^ p=\dfrac {1}{2}<1 \]](images/img-0247.png) |
aqui usou-se o fato que se uma função  é contínua num intervalo que contém os termos da sequência
é contínua num intervalo que contém os termos da sequência 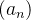 então
então 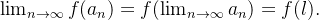 se
se 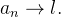 Nesse caso, temos
Nesse caso, temos
![\[ \lim _{n \to \infty } (\dfrac {n+1}{n})^ p=(\lim _{n\to \infty } \dfrac {n+1}{n})^ p=1^ p=1 \]](images/img-0251.png) |
Example 32. Considere a sequência 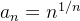 e calcule
e calcule 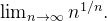
Temos que 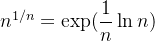 daí
daí
![\[ \lim _{n \to \infty } n^{1/n}=\lim _{n\to \infty }\exp (\dfrac {1}{n}\ln n)=\exp (\lim _{n\to \infty }\dfrac {1}{n}\ln n)=\exp 0=1. \]](images/img-0255.png) |