| Estudo Numérico de algumas EDOs |
O cálculo de (18) pode ser facilmente feito em um programa computacional SIR.py.
from numpy import zeros, linspace
import matplotlib.pyplot as plt
# time out 1h
beta=10.0/(40*8*24)
gamma=3./(15*24)
dt=0.1 # 6 min
D=30 # simulate for D days
N_t=int(D*24/dt) # corresponds numero de horas
t=linspace(0, N_t*dt, N_t+1)
S=zeros(Nt+1)
I=zeros(Nt+1)
R=zeros(Nt+1)
# condições iniciais
S(0)=50
I(0)=1
R(0)=0
# passos das equações avançadas no tempo
for n in range(Nt):
S[n+1]=S[n]-dt*beta*S[n]I[n]
I[n+1]=I[n]+dt*beta*S[n]I[n]-dt*gamma *I[n]
R[n+1]=R[n]+dt*gamma*I[n]
fig=plt.figure()
l1,l2,l3=plt.plot(t,S,t,I,t,R)
fig.legend((l1,l2,l3),(’S’,’I’,’R’),’upper left’)
plt.xlabel(’hours’)
plt.show()
plt.savefig(’tmp.pdf’);plt.savefig(’tmp.png’)
Este programa foi escrito para estudar a disseminação de uma gripe num mencionado internato, e o raciocínio para uma possível escolha de 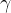 e
e 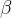 é como segue.Nesta escola onda a doença se espalhou, no começo se observou que haviam 40 suscetíveis e 8 infectados, e esse número se tornou em 30 e 18 após 24 horas.
é como segue.Nesta escola onda a doença se espalhou, no começo se observou que haviam 40 suscetíveis e 8 infectados, e esse número se tornou em 30 e 18 após 24 horas.
Usando o tempo como uma hora por unidade, temos por (3) que 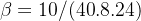 . Entre os 15 infectados notamos que 3 se recuperaram dando
. Entre os 15 infectados notamos que 3 se recuperaram dando 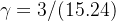 . Aplicando este parâmetro ao novo caso, existem inicialmente 50 suscetíveis e 1 infectado dando o gráfico na figura 1 (observamos que
. Aplicando este parâmetro ao novo caso, existem inicialmente 50 suscetíveis e 1 infectado dando o gráfico na figura 1 (observamos que 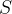 reduziu enquanto
reduziu enquanto 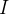 e
e 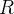 aumentaram. Depois de 30 dias todos que estavam doentes se recuperaram novamente.
aumentaram. Depois de 30 dias todos que estavam doentes se recuperaram novamente.
Podemos experimentar com 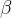 e
e 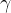 para ver se temos um surto da doença ou não. Imagine que uma campanha de "lavar as mãos" tenha tido um bom sucesso no combate ‘a doença, e neste caso, se experimentou uma redução de
para ver se temos um surto da doença ou não. Imagine que uma campanha de "lavar as mãos" tenha tido um bom sucesso no combate ‘a doença, e neste caso, se experimentou uma redução de 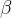 por um fator de 5. Com este valor de
por um fator de 5. Com este valor de 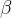 baixo a doença se espalhou bem lentamente se simularmos por 60 dias. As curvas aparecem nas figuras 1 e 2.
baixo a doença se espalhou bem lentamente se simularmos por 60 dias. As curvas aparecem nas figuras 1 e 2.
![\includegraphics[scale=0.3]{gripe.png}](images/img-0081.png)
![\includegraphics[scale=0.7]{gripecontrolada.png}](images/img-0082.png)
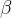 é muito menor que na fig. 1)
é muito menor que na fig. 1)Observação 1. Olhando para a equação de 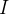 é claro que nós devemos ter
é claro que nós devemos ter 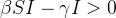 para que
para que 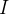 cresça. Quando começamos a simulação significa que
cresça. Quando começamos a simulação significa que
ou simplesmente,
![\[ \beta S(0) I(0)-\gamma I(0)>0 \]](images/img-0084.png)
para crescer o número de infectados e espalhar a doença.Podemos correr o programa SRI.py com
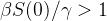
(21)
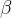 menor que (21)e observamos que não há mais surto.
menor que (21)e observamos que não há mais surto.
Observação 2.
Frequentemente quando desenvolvemos um modelo matemático começamos com um modelo específico e vemos através desse modelo que o que está acontecendo em essência neste exemplo também ocorrerá em muitas configurações de problemas semelhantes.
Nós tentamos incorporar esta generalização no modelo para que o mesmo tenha uma aplicação muito mais ampla do que a que pretendíamos no começo. Este é o próprio poder da modelagem matemática: resolvendo um caso específico, muitas vezes desenvolvemos ferramentas mais genéricas que podem ser prontamente aplicadas para resolver problemas aparentemente diferentes.