| Estudo Numérico de algumas EDOs |
Imagine um internato fora do país. Esta escola é uma sociedade pequena e fechada. De repente, um ou mais dos alunos ficam gripados. Esperamos que a gripe possa se espalhar de forma bastante eficaz ou morrer. A questão é quantos alunos e funcionários da escola serão afetados.
Algumas matemáticas bem simples podem nos ajudar a entender a dinâmica de como a doença se espalha. Deixe a função matemática S(t) contar quantos indivíduos, no tempo t, têm a possibilidade de se infectar. Aqui, t pode contar horas ou dias, por exemplo. Esses indivíduos formam uma categoria denominada suscetíveis, rotulada como S. Outra categoria, eu, consiste nos indivíduos que estão infectados. Deixe I(t) contar quantos há na categoria I no tempo t. Supõe-se que um indivíduo que se recuperou da doença ganhe imunidade.
Há também uma pequena possibilidade de que um infectado morra. Em ambos os casos, o indivíduo é movido da categoria I para uma categoria que chamamos de categoria removida, rotulada com R. Deixamos que R(t) conte o número de indivíduos na categoria R no tempo t. Aqueles que entram na categoria R, não podem sair desta categoria.
Resumindo, a disseminação dessa doença é essencialmente a dinâmica de mover indivíduos da categoria S para a categoria I e depois para a categoria R. Podemos usar a matemática para descrever mais precisamente a troca entre as categorias. A ideia fundamental é descrever as mudanças que ocorrem durante um pequeno intervalo de tempo, denotado por 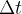 .
.
Nosso modelo de doença é frequentemente referido como um modelo de compartimento, onde as quantidades são embaralhadas entre compartimentos (aqui um sinônimo para categorias) de acordo com algumas regras. As regras expressam mudanças em um pequeno intervalo de tempo 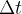 , e a partir dessas mudanças podemos deixar de ir a zero e obter derivativos. As equações resultantes passam então das equações de diferença (com
, e a partir dessas mudanças podemos deixar de ir a zero e obter derivativos. As equações resultantes passam então das equações de diferença (com 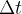 finito) para equações diferenciais (
finito) para equações diferenciais (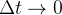 ).
).
Introduzimos uma malha uniforme no tempo, 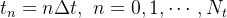 ; e procure
; e procure 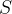 nos pontos da malha. A aproximação numérica de
nos pontos da malha. A aproximação numérica de 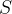 no tempo
no tempo 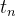 é denotada por
é denotada por 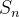 . Da mesma forma, buscamos os valores desconhecidos de
. Da mesma forma, buscamos os valores desconhecidos de 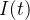 e
e 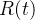 nos pontos de malha e introduzimos uma notação semelhante
nos pontos de malha e introduzimos uma notação semelhante 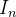 e
e 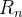 para as aproximações aos valores exatos
para as aproximações aos valores exatos 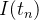 e
e 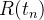 .
.
No intervalo de tempo, sabemos que algumas pessoas serão infectadas, então 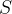 diminuirá. Em breve discutiremos por matemática que haverá
diminuirá. Em breve discutiremos por matemática que haverá 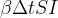 novos indivíduos infectados neste intervalo de tempo, onde
novos indivíduos infectados neste intervalo de tempo, onde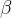 é um parâmetro que reflete como as pessoas são facilmente infectadas durante um intervalo de tempo de duração da unidade.
é um parâmetro que reflete como as pessoas são facilmente infectadas durante um intervalo de tempo de duração da unidade.
Se a perda em 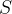 é
é 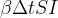 , temos que a mudança em
, temos que a mudança em 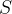 será:
será:
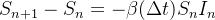 |
(1) |
Dividindo por 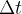 e deixando
e deixando 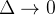 , faz a abordagem do lado esquerdo
, faz a abordagem do lado esquerdo 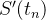 tal que obtemos uma equação diferencial
tal que obtemos uma equação diferencial
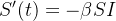 |
(2) |
O raciocínio em ir da equação de diferença (1) para a equação diferencial (2) segue exatamente os passos explicados na seção. 4.1.1. Antes de prosseguir com o desenvolvimento de 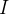 e
e 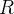 a tempo, vamos explicar a fórmula
a tempo, vamos explicar a fórmula 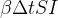 . Temos
. Temos 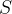 suscetíveis e
suscetíveis e 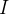 infectadas pessoas.
infectadas pessoas.
Estes podem formar pares 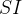 . Agora, suponha que durante um intervalo de tempo
. Agora, suponha que durante um intervalo de tempo 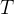 nós medimos que
nós medimos que 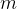 reuniões pareadas reais ocorrem entre
reuniões pareadas reais ocorrem entre 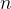 pares de pessoas teoricamente possíveis das categorias
pares de pessoas teoricamente possíveis das categorias 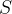 e
e 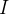 . A probabilidade de que as pessoas se encontrem em pares durante um tempo T é (pela definição de probabilidade empírica de frequência) igual a
. A probabilidade de que as pessoas se encontrem em pares durante um tempo T é (pela definição de probabilidade empírica de frequência) igual a 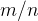 , ou seja, o número de sucessos dividido pelo número de resultados possíveis.
, ou seja, o número de sucessos dividido pelo número de resultados possíveis.
A partir dessas estatísticas, normalmente derivamos quantidades expressas por unidade de tempo, ou seja, aqui queremos a probabilidade por unidade de tempo,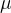 que é encontrada dividindo por
que é encontrada dividindo por 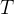 :
: 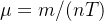 . Dada a probabilidade
. Dada a probabilidade 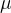 , o número esperado de reuniões por intervalo de tempo de pares possíveis de
, o número esperado de reuniões por intervalo de tempo de pares possíveis de 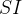 é (a partir de estatísticas básicas)
é (a partir de estatísticas básicas) 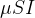 .
.
Durante um intervalo de tempo 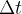 , haverá
, haverá 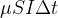 um número esperado de reuniões entre suscetíveis e pessoas infectadas, de modo que o vírus possa se espalhar. Apenas uma fração do
um número esperado de reuniões entre suscetíveis e pessoas infectadas, de modo que o vírus possa se espalhar. Apenas uma fração do 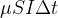 das reuniões são eficazes no sentido de que o suscetível realmente se infecta. Contando que
das reuniões são eficazes no sentido de que o suscetível realmente se infecta. Contando que 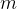 pessoas são infectadas em
pessoas são infectadas em 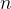 tais reuniões em pares (digamos, 5 estão infectadas de 1000 reuniões),podemos estimar a probabilidade de ser infectado como
tais reuniões em pares (digamos, 5 estão infectadas de 1000 reuniões),podemos estimar a probabilidade de ser infectado como 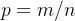 .
.
O número esperado de indivíduos na categoria 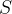 que pegaram o vírus e foram infectados é então
que pegaram o vírus e foram infectados é então 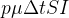 . O valor de
. O valor de 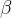 deve ser conhecido para predizer o futuro com o modelo de disseminação. Uma possibilidade é estimar
deve ser conhecido para predizer o futuro com o modelo de disseminação. Uma possibilidade é estimar 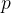 e
e 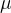 de seus significados na derivação acima.
de seus significados na derivação acima.
Alternativamente, podemos observar um experimento existem 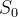 suscetíveis e
suscetíveis e 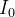 infectados em algum momento no tempo. Durante um intervalo de tempo
infectados em algum momento no tempo. Durante um intervalo de tempo 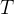 nós contamos que
nós contamos que 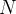 suscetíveis foram infectados.
suscetíveis foram infectados.
Usando (1) como uma rude aproximação de como S se desenvolveu durante o tempo 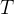 (e agora
(e agora 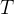 não é necessariamente pequeno, mas nós usamos (1) de todo jeito), obtemos
não é necessariamente pequeno, mas nós usamos (1) de todo jeito), obtemos
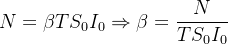 |
(3) |
Nós necessitamos de uma equação adicional para descrever a evolução de 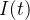 . Tal equação é fácil de estabelecer notando que uma perda na categoria de
. Tal equação é fácil de estabelecer notando que uma perda na categoria de 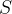 representa um ganho na categoria de
representa um ganho na categoria de 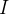 . Mais precisamente,
. Mais precisamente,
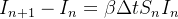 |
(4) |
Contudo existe também uma perda na categoria 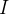 ja que houve pessoas que se recuperaram da doença.
ja que houve pessoas que se recuperaram da doença.
Suponha que podemos medir que 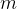 de
de 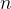 indivíduos se recuperaram num período de tempo
indivíduos se recuperaram num período de tempo 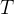 (digamos 10 de 40 doentes se recuperaram durante um dia: m=10, n=40, T=24 h. Agora
(digamos 10 de 40 doentes se recuperaram durante um dia: m=10, n=40, T=24 h. Agora 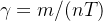 é a probabilidade que um indivíduo recuperar-se num certo intervalo de tempo. Então(em média)
é a probabilidade que um indivíduo recuperar-se num certo intervalo de tempo. Então(em média) 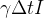 infectados irão se recuperar num intervalo de tempo
infectados irão se recuperar num intervalo de tempo 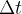 .
.
Esta quantidade representa uma perda na categoria 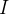 e um ganho na categoria
e um ganho na categoria 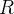 , podemos então escrever a mudança total na categoria
, podemos então escrever a mudança total na categoria 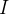 como
como
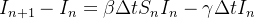 |
(5) |
A mudança na categoria 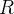 é simples: existe sempre um crescimento que vem da categoria
é simples: existe sempre um crescimento que vem da categoria 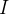 :
:
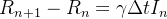 |
(6) |
Não há perda na categoria 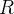 (pessoas são ou recuperadas ou imunes ou mortas. Finalizamos assim a modelagem dessa categoria. Nós não precisamos estritamente da equação (6) para
(pessoas são ou recuperadas ou imunes ou mortas. Finalizamos assim a modelagem dessa categoria. Nós não precisamos estritamente da equação (6) para 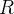 . Mas extensões do modelo serão necessárias mais tarde para a equação de
. Mas extensões do modelo serão necessárias mais tarde para a equação de 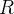 .
.
Dividindo por 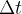 nas equações (5) e (6) e fazendo
nas equações (5) e (6) e fazendo 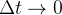 resulta nas correspondentes equações diferenciais
resulta nas correspondentes equações diferenciais
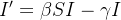 |
(7) |
e
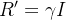 |
(8) |
Para referência, listamos um conjunto completo dos três equações de diferença:
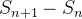 |
 |
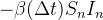 |
(9) | ||
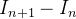 |
 |
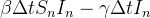 |
(10) | ||
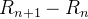 |
 |
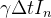 |
(11) |
Observe que isolamos as novas quantidades desconhecidas 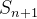 ,
, 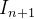 e
e 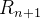 no lado esquerdo, de modo que elas possam ser prontamente computadas se
no lado esquerdo, de modo que elas possam ser prontamente computadas se 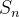 ,
, 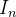 e
e 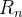 forem conhecidos. Para iniciar esse procedimento, precisamos saber
forem conhecidos. Para iniciar esse procedimento, precisamos saber 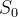 ,
, 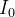 ,
, 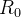 . Obviamente, também precisamos ter valores para os parâmetros
. Obviamente, também precisamos ter valores para os parâmetros 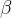 e
e 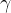 .
.
Também listamos o sistema de três equações diferenciais:
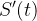 |
 |
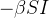 |
(12) | ||
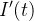 |
 |
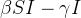 |
(13) | ||
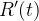 |
 |
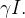 |
(14) |
Este modelo de equação assim como sua parte discreta, acima mencionada, é conhecido como modelo SIR. Os dados de entrada para esse modelo de equações diferenciais são 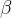 e
e 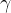 bem como suas condições iniciais
bem como suas condições iniciais 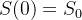 ,
, 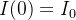 e
e 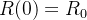 .
.