1.2 Um método de Euler avançado para um sistema de edo

Vamos aplicar o mesmo principio feito na secao 411 para discretizar o sistema de equações diferenciais usando o método avançado de Euler. Nós já temos uma malha no tempo e uma quantidade discreta no tempo 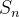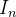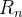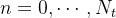$S_ n$ , $I_ n$ , $R_ n$ , $n=0,\cdots , N_ t$ . As três equações diferenciais são consideradas válidas nos pontos da malha.

No ponto 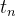$t_ n$ então temos

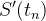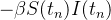$\displaystyle S’(t_ n)$	$\displaystyle =$	$\displaystyle -\beta S(t_ n) I(t_ n)$	(15)
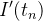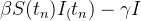$\displaystyle I’(t_ n)$	$\displaystyle =$	$\displaystyle \beta S(t_ n) I_(t_ n)-\gamma I$	(16)
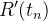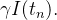$\displaystyle R’(t_ n)$	$\displaystyle =$	$\displaystyle \gamma I(t_ n).$	(17)

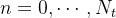para $n=0,\cdots , N_ t$ .

Esta é uma aproximação válida desde que as equações diferenciais são originalmente válidas em todo tempo 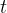$t$ (usualmente em algum intervalo finito $[0,T]$ ).

Usando diferenças avançadas finitas para as derivadas em uma aproximação adicional,

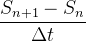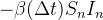$\displaystyle \label{edo26} \dfrac {S_{n+1}-S_ n}{\Delta t}$	$\displaystyle =$	$\displaystyle -\beta (\Delta t) S_ n I_ n$	(18)
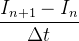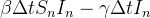$\displaystyle \dfrac {I_{n+1}-I_ n}{\Delta t}$	$\displaystyle =$	$\displaystyle \beta \Delta t S_ n I_ n-\gamma \Delta t I_ n$	(19)
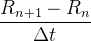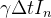$\displaystyle \dfrac {R_{n+1}-R_ n}{\Delta t}$	$\displaystyle =$	$\displaystyle \gamma \Delta t I_ n$	(20)

Como podemos ver essas equações são idênticas às equações de diferenças que naturalmente surgem na derivação do modelo. Contudo, outros métodos numéricos, além do método avançado de Euler, resultarão em pequenas diferenças das equações de diferenças finitas.