| Estudo Numérico de algumas EDOs |
Quando temos uma equação diferencial específica com um valor desconhecido, então rapidamente nos tornamos para uma equação diferencial abstrata escrita na forma genérica 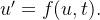
Uma específica equação corresponde a uma escolha específica da fórmula 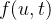 envolvendo
envolvendo 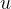 e opcionalmente
e opcionalmente 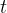 . É vantajoso também escrever um sistema de equações diferenciais na forma abstrata,
. É vantajoso também escrever um sistema de equações diferenciais na forma abstrata,
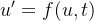 |
(22) |
mas desde que se entenda que 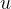 agora é um vetor de funções e
agora é um vetor de funções e 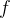 também. Dizemos nesse caso, que a equação (22) é um sistema de EDO. Para o caso do modelo SIR introduzimos o vetor tridimensional, dado por
também. Dizemos nesse caso, que a equação (22) é um sistema de EDO. Para o caso do modelo SIR introduzimos o vetor tridimensional, dado por
![\[ u=(S(t), I(t), R(t)) \]](images/img-0091.png) |
e, por outro lado, temos que 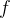 fica dado por
fica dado por
![\[ f(u,t)=(-\beta SI, \beta SI-\gamma I, \gamma I). \]](images/img-0092.png) |
Desde que 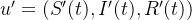 , obtemos que
, obtemos que 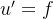 significa
significa
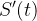 |
 |
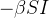 |
(23) | ||
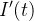 |
 |
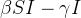 |
(24) | ||
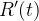 |
 |
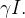 |
(25) |
A pequena notação 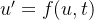 é muito útil desde que possamos derivar e implementar os métodos numéricos para este sistema abstrato e em aplicações específicas basta identificar a fórmula no vetor
é muito útil desde que possamos derivar e implementar os métodos numéricos para este sistema abstrato e em aplicações específicas basta identificar a fórmula no vetor 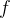 , implementá-las e chamar a funcionalidade que resolve o sistema de equações diferenciais.
, implementá-las e chamar a funcionalidade que resolve o sistema de equações diferenciais.
Em Python o método de Euler avançado
![\[ u_{n+1}=u_ n+\Delta t f(u_ n,t_ n) \]](images/img-0096.png) |
sendo um escalar ou vetor, pode ser codificado como
![\[ u[n+1]=u[n]+dt* f(u[n],t[n]) \]](images/img-0097.png) |
ambos no caso escalar ou vetorial. No caso vetorial, ![$u[n]$](images/img-0098.png) é um unidimensional numpy array de comprimento
é um unidimensional numpy array de comprimento 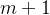 mantendo a quantidade matemática
mantendo a quantidade matemática 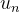 e a função Python
e a função Python 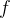 deve retornar uma numpy array de comprimento
deve retornar uma numpy array de comprimento 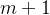 .
.
Para tudo isso funcionar a solução numérica completa deve ser representada por uma array bidimensional criada por 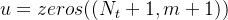 o primeiro índice conta os pontos do tempo e o segundo conta as componentes do vetor solução num mesmo ponto. Isto é,
o primeiro índice conta os pontos do tempo e o segundo conta as componentes do vetor solução num mesmo ponto. Isto é, ![$u[n,i]$](images/img-0102.png) corresponde a quantidade matemática
corresponde a quantidade matemática 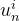 . Quando usamos somente um símbolo, como em
. Quando usamos somente um símbolo, como em ![$u[n]$](images/img-0098.png) , isso é o mesmo que
, isso é o mesmo que ![$u[n,:]$](images/img-0104.png) , selecionamos todos os componentes da solução no ponto de tempo com o índice
, selecionamos todos os componentes da solução no ponto de tempo com o índice 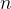 .
.
Então a tarefa ![$u[n+1]=\cdots $](images/img-0105.png) torna-se correta pois ela é está realmente no lugar da tarefa
torna-se correta pois ela é está realmente no lugar da tarefa ![$u[n+1,:]=\cdots $](images/img-0106.png) A boa característica desses fatos é que a mesma parte do código Python funciona tanto para um edo escalar quanto para um sistema de edos. Veja o programa numérico para o sistema de edos:
A boa característica desses fatos é que a mesma parte do código Python funciona tanto para um edo escalar quanto para um sistema de edos. Veja o programa numérico para o sistema de edos:
from numpy import zeros, linspace, asarray
import matplotlib.pyplot as plt
def EDO_FE(f, U0, dt,T):
Nt=int(round(float(T)/dt))
#garantir que qualquer lista / tupla retornada de f seja empacotada como array
f_= lambda u,t: asarray(f(u,t))
u=zeros((Nt+1, len(U0)))
t=linspace(0,Nt*dt,len(u))
u[0]=U0
for n in range(Nt):
u[n+1]=u[n]+dt*f_(u[n],t[n])
return u,t
The line f_= lambda merece uma explanação: para o usuário que só precisa definir 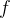 no sistema de edo, é conveniente inserir várias expressões matemáticas no lado direito da lista e esperar o retorno daquela lista. Obviamente poderíamos exigir que o usuário convertesse a lista em uma numpy matriz.
no sistema de edo, é conveniente inserir várias expressões matemáticas no lado direito da lista e esperar o retorno daquela lista. Obviamente poderíamos exigir que o usuário convertesse a lista em uma numpy matriz.
Mas é tão fácil fazer uma conversão geral na função da edo_FE. Para ter certeza que o resultado para 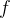 é na verdade uma matriz que pode ser usada no cálculo de matriz na fórmula
é na verdade uma matriz que pode ser usada no cálculo de matriz na fórmula ![$u[n+1]=u[n]+dt*f\_ (u[n],t[n])$](images/img-0107.png) , introduzimos uma nova função f_ que chama a
, introduzimos uma nova função f_ que chama a 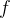 do usuário e envia o resultado através da numpy function array, que assegura que este argumento é convertido a uma matriz numpy (se ela já não for uma matriz).
do usuário e envia o resultado através da numpy function array, que assegura que este argumento é convertido a uma matriz numpy (se ela já não for uma matriz).
Note também que parênteses extras são requeridos quando chamamos zeros com dois índices.
Vamos mostrar como o modelo SIR pode ser resolvido usando o caso geral dado acima que resolve sobre qualquer edo de vetores. Implementação para 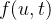 . def f(u,t):
. def f(u,t):
S,I,R=u
return(-beta*S*I, beta*S*I-gamma*I, gamma*I)
Note que os valores de 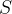 ,
, 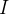 e
e 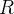 correspondem a
correspondem a 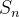 ,
, 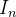 e
e 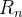 . Esses valores são justamente atribuidos nas várias fórmulas da edo vetorial. Aqui nós coletamos os valores em uma lista, uma vez que a edo irá de qualquer maneira quebrar essa lista em uma matriz. Podemos então retornar uma matriz em vez disso.
. Esses valores são justamente atribuidos nas várias fórmulas da edo vetorial. Aqui nós coletamos os valores em uma lista, uma vez que a edo irá de qualquer maneira quebrar essa lista em uma matriz. Podemos então retornar uma matriz em vez disso.
def f(u,t):
S,I,R=u
return array([-beta*S*I, beta*S*I-gamma*I, gamma*I])
A versão da lista parece melhor, então é por isso que preferimos uma lista e, em vez disso, introduzimos f_ = lambda u,t: asarray(f(u,t)) no programa abstrato geral. Consideremos a seguinte implementação:
def Demo_SIR():
”’ Test case use SIR model”’ def f(u,t):
S,I,R=u
return[-beta*S*I, beta*S*I-gamma*I, gamma*I]
beta=10/(40*8*24)
gamma=3./(15*24)
dt=0.1
D=30
Nt=int(D*24/dt)
T=dt*Nt)
U0=[50,1,0]
u,t=edo_FE(f,U0,dt,T)
S=u[:,0]
I=u[:,1]
R=u[:,2]
fig=plt.figure()
l1,l2,l3=plt.plot(t,S,t,I,t,R)
fig.legend((l1,12,l3), (’S’, ’I’, ’R’),’lower right’)
plt.xlabel(’horas’)
plt.show()
N= S[0]+I[0]+R[0]
eps=1E-12)
for n in range(len(S)):
SIR_ sum=S[n]+I[n]+R[n]
if abs(SIR_ sum-N)>eps:)
print("consistence falhou: S+I+R=%g !=% g" %(SIR_ sum,N))
if__name__==’__main__’:)
Demo_SIR()
Lembre-se que o 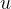 retornado da edo_FE contém todas as componentes (S,I,R) na solução vetorial em todos os pontos do tempo. Precisamos portanto extrair os valores de S, I e R em matrizes separadas para outras análises e fácil plotagem. Outra característica fundamental deste código de alta-qualidade é a verificação de consistência.
retornado da edo_FE contém todas as componentes (S,I,R) na solução vetorial em todos os pontos do tempo. Precisamos portanto extrair os valores de S, I e R em matrizes separadas para outras análises e fácil plotagem. Outra característica fundamental deste código de alta-qualidade é a verificação de consistência.
Adicionando as três equações diferenciais no SIR model, vemos que 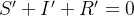 , o que significa que
, o que significa que 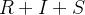 é constante, podemos checar que essa relação permanece por comparar
é constante, podemos checar que essa relação permanece por comparar 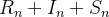 com a soma das condições iniciais. a checagem não é uma verificação completa, mas é melhor que não fazer nada e esperar que os cálculos computacionais estejam corretos. O exercício 4.5 sugere um outro método para controlar a qualidade da solução numérica.
com a soma das condições iniciais. a checagem não é uma verificação completa, mas é melhor que não fazer nada e esperar que os cálculos computacionais estejam corretos. O exercício 4.5 sugere um outro método para controlar a qualidade da solução numérica.