| Cálculo Diferencial e Integral 3 |
 cie paramétrica
cie paramétricaSeja  uma superf
uma superf cie paramétrica representada pela função
cie paramétrica representada pela função  definida numa região
definida numa região 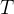 do plano
do plano Um retângulo em
Um retângulo em 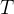 de área
de área 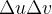 é aplicado por
é aplicado por  sobre um paralelogramo curvil
sobre um paralelogramo curvil neo em
neo em  com área aproximadamente igual a
com área aproximadamente igual a
![\[ \left\Vert \dfrac {\partial \mathbf{r}}{\partial u}\times \dfrac {\partial \mathbf{r}}{\partial v}\right\Vert \Delta u\Delta v. \]](images/img-1033.png) |
Definição: A área de 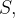 que representamos por
que representamos por  se define pela integral dupla
se define pela integral dupla
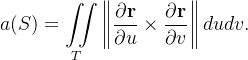 |
(8) |
Ou seja,
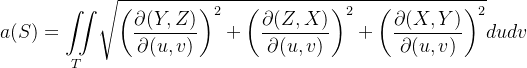 |
(9) |
Se  vem dada explicitamente por uma equação da forma
vem dada explicitamente por uma equação da forma  então
então
![\[ \left\Vert \dfrac {\partial \mathbf{r}}{\partial x}\times \dfrac {\partial \mathbf{r}}{\partial y}\right\Vert =\left\Vert -\frac{\partial f}{\partial x}\mathbf{i}-\frac{\partial f}{\partial y}\mathbf{j}+\mathbf{k}\right\Vert =\sqrt{1+\left( \frac{\partial f}{\partial x}\right) ^{2}+\left( \frac{\partial f}{\partial y}\right) ^{2}}. \]](images/img-1039.png) |
Nesse caso,
![\[ a(S)={\displaystyle \iint \limits _{T}} \sqrt{1+\left( \frac{\partial f}{\partial x}\right) ^{2}+\left( \frac{\partial f}{\partial y}\right) ^{2}}dxdy, \]](images/img-1040.png) |
onde 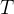 é a projeção de
é a projeção de  no plano-
no plano-
![\includegraphics[ height=3.7861in, width=3.5838in ]{Figura6.eps}](images/img-1042.png)
Quando  está num plano paralelo ao plano-
está num plano paralelo ao plano- a função
a função  é constante e temos
é constante e temos  e
e  da
da
![\[ a(S)={\displaystyle \iint \limits _{T}} dxdy. \]](images/img-1046.png) |
Em cada ponto de  , seja
, seja  onde
onde 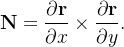 Como a componente
Como a componente  de
de  é
é  temos
temos
![\[ \cos \gamma =\frac{\mathbf{N\cdot k}}{\left\Vert \mathbf{N}\right\Vert \left\Vert \mathbf{k}\right\Vert }=\frac{1}{\left\Vert \mathbf{N}\right\Vert }=\frac{1}{\left\Vert \dfrac {\partial \mathbf{r}}{\partial x}\times \dfrac {\partial \mathbf{r}}{\partial y}\right\Vert }. \]](images/img-1050.png) |
Portanto,  Logo,
Logo,
![\[ a(S)={\displaystyle \iint \limits _{T}} \frac{1}{\cos \gamma }dxdy. \]](images/img-1052.png) |
Se  está num plano não perpendicular ao plano-
está num plano não perpendicular ao plano- . Neste caso,
. Neste caso,  constante e temos que
constante e temos que 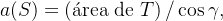 ou
ou
![\[ a(S)=\frac{1}{\cos \gamma }{\displaystyle \iint \limits _{T}} dxdy. \]](images/img-1055.png) |
Agora se  vem dada implicitamente por
vem dada implicitamente por 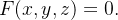 Se
Se  pode projetar-se injetivamente sobre o plano-
pode projetar-se injetivamente sobre o plano- a equação
a equação  define
define  como função de
como função de  e
e 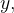 seja
seja  assim
assim
![\[ \frac{\partial f}{\partial x}=-\frac{\partial F}{\partial x}/\frac{\partial F}{\partial z}\text { e }\frac{\partial f}{\partial y}=-\frac{\partial F}{\partial y}/\frac{\partial F}{\partial z} \]](images/img-1058.png) |
nos pontos onde 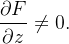 Desse modo
Desse modo
 |
(10) |
Exemplo 1: Área de um hemisfério. Consideremos um hemisfério  de raio
de raio 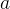 e centro na origem. Temos a representação impl
e centro na origem. Temos a representação impl cita
cita 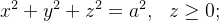 a expl
a expl cita
cita  e a paramétrica
e a paramétrica
![\[ \mathbf{r}(u,v)=a\cos u\ \cos v\mathbf{i}+a\operatorname {sen}u\ \cos v\mathbf{j}+a\operatorname {sen}v\mathbf{k.} \]](images/img-1063.png) |
Para calcular a área de  a partir da representação impl
a partir da representação impl cita utilizamos a fórmula (10) tomando
cita utilizamos a fórmula (10) tomando
![\[ F(x,y,z)=x^{2}+y^{2}+z^{2}-a^{2}. \]](images/img-1064.png) |
Temos que 
 O hemisfério se projeto de forma injetiva no disco
O hemisfério se projeto de forma injetiva no disco  do plano-
do plano- Não podemos aplica a fórmula diretamente pois
Não podemos aplica a fórmula diretamente pois  é nula na fronteira de
é nula na fronteira de 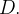 Mas tal derivada não é nula em todo ponto no interior de
Mas tal derivada não é nula em todo ponto no interior de 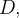 assim consideramos um disco concêntrico
assim consideramos um disco concêntrico  de raio
de raio 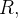
 Se
Se  representa a porção correspondente do hemisfério superior,
representa a porção correspondente do hemisfério superior,  é aplicável e resulta:
é aplicável e resulta:
![\[ \text {\'{a}rea de }S(R)={\displaystyle \iint \limits _{D(R)}} \frac{\sqrt{\left( 2x\right) ^{2}+\left( 2y\right) ^{2}+\left( 2z\right) ^{2}}}{\left\vert 2z\right\vert }dxdy \]](images/img-1074.png) |
![\[ ={\displaystyle \iint \limits _{D(R)}} \frac{a}{z}dxdy=a{\displaystyle \iint \limits _{D(R)}} \frac{1}{\sqrt{a^{2}-x^{2}-y^{2}}}dxdy \]](images/img-1075.png) |
temos
![\[ \text {\'{a}rea de }S(R)=a\int _{0}^{2\pi }\left[ \int _{0}^{R}\frac{1}{\sqrt{a^{2}-r^{2}}}rdr\right] d\theta =2\pi a\left( a-\sqrt{a^{2}-R^{2}}\right) \]](images/img-1076.png) |
Quando 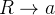 então área de
então área de  No caso da superf
No caso da superf cie parametrizada, temos
cie parametrizada, temos
![\[ \left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert =\left\Vert a\cos v\ \mathbf{r}(u,v)\right\Vert =a^{2}\left\vert \cos v\right\vert \]](images/img-1079.png) |
Logo, podemos aplicar  tomando
tomando ![$T=\left[ 0,2\pi \right] \times \left[ 0,\frac{1}{2}\pi \right] .$](images/img-1081.png) Obtemos
Obtemos
![\[ a(S)=a^{2}{\displaystyle \iint \limits _{T}} \left\vert \cos v\right\vert dudv=a^{2}\int _{0}^{2\pi }\left[ \int _{0}^{\dfrac {\pi }{2}}\cos vdv\right] du=2\pi a^{2}. \]](images/img-1082.png) |