| Cálculo Diferencial e Integral 3 |
Considere uma superf cie representada por
cie representada por
![\[ S:\ \mathbf{r}(u,v)=X\left( u,v\right) \mathbf{i}+Y\left( u,v\right) \mathbf{j}+Z\left( u,v\right) \mathbf{k,\ }\left( u,v\right) \in T \]](images/img-0983.png) |
Se 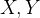 e
e 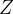 são deriváveis em
são deriváveis em 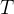 podemos considerar os dois vetores
podemos considerar os dois vetores
![\[ \frac{\partial \mathbf{r}}{\partial u}=\frac{\partial X}{\partial u}\mathbf{i}+\frac{\partial Y}{\partial u}\mathbf{j+}\frac{\partial Z}{\partial u}\mathbf{k} \]](images/img-0986.png) |
e
![\[ \frac{\partial \mathbf{r}}{\partial v}=\frac{\partial X}{\partial v}\mathbf{i}+\frac{\partial Y}{\partial v}\mathbf{j+}\frac{\partial Z}{\partial v}\mathbf{k} \]](images/img-0987.png) |
O produto vetorial  se denominará produto vetorial fundamental de
se denominará produto vetorial fundamental de 
 |
![$\displaystyle =\left\vert \begin{array}[c]{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \begin{array}[c]{c}\frac{\partial X}{\partial u}\\ \end{array}& \begin{array}[c]{c}\frac{\partial Y}{\partial u}\\ \end{array}& \begin{array}[c]{c}\frac{\partial Z}{\partial u}\\ \end{array}\\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v} & \frac{\partial Z}{\partial v}\end{array} \right\vert =\left\vert \begin{array}[c]{cc}\begin{array}[c]{c}\frac{\partial Y}{\partial u}\\ \end{array}& \begin{array}[c]{c}\frac{\partial Z}{\partial u}\\ \end{array}\\ \frac{\partial Y}{\partial v} & \frac{\partial Z}{\partial v}\end{array} \right\vert \mathbf{i}+\left\vert \begin{array}[c]{cc}\begin{array}[c]{c}\frac{\partial Z}{\partial u}\\ \end{array}& \begin{array}[c]{c}\frac{\partial X}{\partial u}\\ \end{array}\\ \frac{\partial Z}{\partial v} & \frac{\partial X}{\partial v}\end{array} \right\vert \mathbf{j}+\left\vert \begin{array}[c]{cc}\begin{array}[c]{c}\frac{\partial X}{\partial u}\\ \end{array}& \begin{array}[c]{c}\frac{\partial Y}{\partial u}\\ \end{array}\\ \frac{\partial X}{\partial v} & \frac{\partial Y}{\partial v}\end{array} \right\vert \mathbf{k} $](images/img-0991.png) |
|||
 |
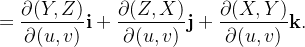 |
Se 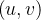 é um ponto em
é um ponto em 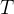 no qual
no qual  e
e 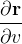 são cont
são cont nuas e o produto vetorial fundamental não é nulo, então o ponto imagem
nuas e o produto vetorial fundamental não é nulo, então o ponto imagem 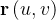 se chama ponto regular de
se chama ponto regular de 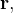 caso contrário, o ponto é dito ponto singular
caso contrário, o ponto é dito ponto singular Uma superf
Uma superf cie
cie 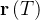 se chama regular se todos os seus pontos são regulares.
se chama regular se todos os seus pontos são regulares.
Um retângulo em 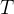 que tenha uma área
que tenha uma área 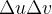 se converte numa porção em
se converte numa porção em 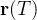 que aproximamos por um paralelogramo determinado pelos vetores
que aproximamos por um paralelogramo determinado pelos vetores 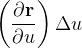 e
e 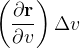 . A área desse paralelogramo é o módulo do produto vetorial
. A área desse paralelogramo é o módulo do produto vetorial
![\[ \left\Vert \dfrac {\partial \mathbf{r}}{\partial u}\Delta u\times \dfrac {\partial \mathbf{r}}{\partial v}\Delta v\right\Vert =\left\Vert \dfrac {\partial \mathbf{r}}{\partial u}\times \dfrac {\partial \mathbf{r}}{\partial v}\right\Vert \Delta u\Delta v. \]](images/img-1000.png) |
Em cada ponto regular os vetores  e
e 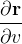 determinam um plano que tem o vetor
determinam um plano que tem o vetor  como normal. Por esta razão o plano determinado por
como normal. Por esta razão o plano determinado por  e
e 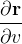 se chama plano tangente à superf
se chama plano tangente à superf cie. A continuidade de
cie. A continuidade de  e
e 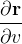 implica na continuidade de
implica na continuidade de  isto significa que o plano tangente se move continuamente numa superf
isto significa que o plano tangente se move continuamente numa superf cie regular. Assim, a continuidade de
cie regular. Assim, a continuidade de  e
e 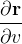 evita a presença de bicos ou arestas nas superf
evita a presença de bicos ou arestas nas superf cies, o fato de
cies, o fato de 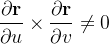 evita os casos degenerados.
evita os casos degenerados.
![\includegraphics[ height=2.3194in, width=5.1526in ]{Figura11.eps}](images/img-1003.png)
Exemplo 3: Superf cies com representação expl
cies com representação expl cita,
cita, 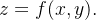 Neste caso,
Neste caso,
![\[ \mathbf{r}(x,y)=x\mathbf{i}+y\mathbf{j}+f(x,y)\mathbf{k,\ }(x,y)\in R \]](images/img-1004.png) |
A região  denomina-se a projeção da superf
denomina-se a projeção da superf cie sobre o plano
cie sobre o plano
![\includegraphics[ height=3.6668in, width=4.088in ]{Figura2.eps}](images/img-1005.png)
Temos que
![\[ \frac{\partial \mathbf{r}}{\partial x}=\mathbf{i}+\frac{\partial f}{\partial x}\mathbf{k},\ \ \frac{\partial \mathbf{r}}{\partial y}=\mathbf{i}+\frac{\partial f}{\partial y}\mathbf{k,}\text { supondo }f\text { diferenci\'{a}vel} \]](images/img-1006.png) |
o que nos dá
![\[ \dfrac {\partial \mathbf{r}}{\partial x}\times \dfrac {\partial \mathbf{r}}{\partial y}=\left\vert \begin{array}[c]{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ 1 & 0 & \frac{\partial f}{\partial x}\\ 0 & 1 & \frac{\partial f}{\partial y}\end{array} \right\vert =-\frac{\partial f}{\partial x}\mathbf{i}-\frac{\partial f}{\partial y}\mathbf{j}+\mathbf{k.} \]](images/img-1007.png) |
Posto que a componente  de
de 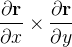 é
é  o produto vetorial fundamental nunca é zero. Logo os únicos pontos singulares desta representação são os pontos onde
o produto vetorial fundamental nunca é zero. Logo os únicos pontos singulares desta representação são os pontos onde 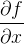 e
e 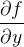 não são cont
não são cont nuas.
nuas.
Um caso t pico é a equação
pico é a equação  que representa um hemisfério de raio
que representa um hemisfério de raio 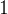 e centro na origem, se
e centro na origem, se  A equação vetorial é
A equação vetorial é
![\[ \mathbf{r}(x,y)=x\mathbf{i}+y\mathbf{j}+\sqrt{1-x^{2}-y^{2}}\mathbf{k} \]](images/img-1014.png) |
ela aplica o disco unitário  sobre o hemisfério e tal aplicação é injetora.
sobre o hemisfério e tal aplicação é injetora.  As derivadas parciais
As derivadas parciais 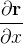 e
e  existem e são cont
existem e são cont nuas em todo o interior do disco, mas não existem na fronteira do disco. Logo, todo ponto da fronteira é um ponto singular desta representação.
nuas em todo o interior do disco, mas não existem na fronteira do disco. Logo, todo ponto da fronteira é um ponto singular desta representação.
Exemplo 4: Consideremos o mesmo hemisfério do exemplo anterior, mas desta vez como imagem do retângulo ![$T=\left[ 0,2\pi \right] \times \left[ 0,\dfrac {\pi }{2}\right] $](images/img-1018.png)
 através da aplicação
através da aplicação
![\[ \ \mathbf{r}(u,v)=a\cos u\cos v\mathbf{i}+a\operatorname {sen}u\cos v\mathbf{j}+a\operatorname {sen}v\mathbf{k} \]](images/img-1019.png) |
os vetores  e
e 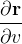 vem dados pelas fórmulas
vem dados pelas fórmulas
![\[ \dfrac {\partial \mathbf{r}}{\partial u}=-a\operatorname {sen}v\cos v\mathbf{i}+a\cos u\cos v\mathbf{j} \]](images/img-1020.png) |
![\[ \dfrac {\partial \mathbf{r}}{\partial v}=-a\cos u\ \operatorname {sen}v\mathbf{i}-a\operatorname {sen}u\operatorname {sen}v\mathbf{j}+a\cos v\mathbf{k} \]](images/img-1021.png) |
Temos que
![\[ \dfrac {\partial \mathbf{r}}{\partial u}\times \dfrac {\partial \mathbf{r}}{\partial v}=a\cos v\mathbf{r}(u,v) \]](images/img-1022.png) |
A imagem de 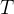 não é uma superf
não é uma superf cie paramétrica simples pois esta aplicação não é injetora. Com efeito, todo ponto do segmento retil
cie paramétrica simples pois esta aplicação não é injetora. Com efeito, todo ponto do segmento retil neo
neo 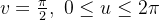 se aplica no ponto
se aplica no ponto  (pólo norte). Também pela periodicidade do seno e cosseno,
(pólo norte). Também pela periodicidade do seno e cosseno,  toma os mesmos valores nos pontos
toma os mesmos valores nos pontos 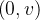 e
e 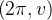 de modo que os lados esquerdo e direito de
de modo que os lados esquerdo e direito de 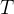 se aplicam na mesma curva, que é um arco que o une o pólo norte ao ponto
se aplicam na mesma curva, que é um arco que o une o pólo norte ao ponto 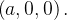 Os vetores
Os vetores  e
e 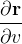 são cont
são cont nuos em todo
nuos em todo 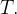 Como
Como 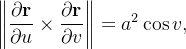 então os únicos pontos singulares desta representação se apresenta quando
então os únicos pontos singulares desta representação se apresenta quando 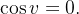 Logo o único ponto singular é o pólo norte.
Logo o único ponto singular é o pólo norte.