| Cálculo Diferencial e Integral 3 |
 cie
cieDefinicao: Seja  uma superf
uma superf cie paramétrica descrita por uma função diferenciável
cie paramétrica descrita por uma função diferenciável  definida em
definida em 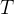 do plano-
do plano- e seja
e seja  um campo escalar definido e limitado em
um campo escalar definido e limitado em  A integral de superf
A integral de superf cie de
cie de  sobre
sobre 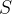 se representa por
se representa por  (ou por
(ou por  ) e é definida como
) e é definida como
![\[ {\displaystyle \iint \limits _{S}} fdS={\displaystyle \iint \limits _{T}} f(\mathbf{r}\left( u,v\right) )\left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert dudv. \]](images/img-1087.png) |
Exemplo 1: Área de superf cie
cie
![\[ {\displaystyle \iint \limits _{S}} dS={\displaystyle \iint \limits _{T}} \left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert dudv. \]](images/img-1088.png) |
Exemplo 2: Fluxo de um fluido através de uma superf cie. Imagine que um flu
cie. Imagine que um flu do é uma coleção de pontos chamados part
do é uma coleção de pontos chamados part culas. A cada part
culas. A cada part cula
cula  corresponde um vetor
corresponde um vetor  chamado velocidade. Este é o campo de velocidade da corrente. O campo de velocidade pode ou não mudar com o tempo. Consideraremos as correntes estacionárias. Seja
chamado velocidade. Este é o campo de velocidade da corrente. O campo de velocidade pode ou não mudar com o tempo. Consideraremos as correntes estacionárias. Seja  a densidade (massa por unidade de volume) do flu
a densidade (massa por unidade de volume) do flu do em
do em 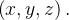 Se o flu
Se o flu do é incompress
do é incompress vel a densidade
vel a densidade  será constante em todo flu
será constante em todo flu do. O produto da densidade pela velocidade representamos por
do. O produto da densidade pela velocidade representamos por 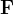
![\[ \mathbf{F}(x,y,z)=\rho \left( x,y,z\right) \mathbf{v}\left( x,y,z\right) \ \ \left( \text {densidade de fluxo da corrente}\right) \]](images/img-1093.png) |
O vetor  tem a mesma direção da velocidade e suas medidas de dimensões são
tem a mesma direção da velocidade e suas medidas de dimensões são
![\[ \frac{\text {massa}}{\text {unid. vol.}}\cdot \frac{\text {distancia}}{\text {unid. tempo}}=\frac{\text {massa}}{\text {unid. \'{a}rea}\cdot \text {unid. tempo}}. \]](images/img-1095.png) |
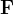 nos diz quanta massa de flu
nos diz quanta massa de flu do circula no ponto
do circula no ponto  na direção de
na direção de  por unidade de área e de tempo.
por unidade de área e de tempo.
Seja  uma superf
uma superf cie paramétrica simples. Em cada ponto regular de
cie paramétrica simples. Em cada ponto regular de 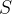 designamos por
designamos por  o vetor unitário normal que tenha o mesmo sentido que o produto vetorial fundamental. Isto é
o vetor unitário normal que tenha o mesmo sentido que o produto vetorial fundamental. Isto é
![\[ \mathbf{\eta }\text { }=\frac{\frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}}{\left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert } \]](images/img-1099.png) |
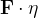
 é a componente do vetor densidade de fluxo na direção
é a componente do vetor densidade de fluxo na direção  . A massa de flu
. A massa de flu do que passa através de
do que passa através de 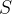 na unidade de tempo na direção de
na unidade de tempo na direção de  se define por
se define por
![\[ {\displaystyle \iint \limits _{\mathbf{r}\left( T\right) }} \mathbf{F\cdot \eta }dS={\displaystyle \iint \limits _{T}} \mathbf{F\cdot \eta }\left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert dudv. \]](images/img-1101.png) |