5.2 Mudança de variável em coordenadas esféricas

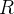Suponha $R$ seja uma região do espaço onde está definida uma função 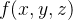$f(x,y,z)$ então o teorema de mudança de variáveis em coordenadas esféricas nos afirma que

${\displaystyle \iiint _{R}} f(x,y,z)dxdydz={\displaystyle \iiint _{R_{1}}} f(\rho \operatorname {sen}\phi \cos \theta ,\rho \operatorname {sen}\phi \operatorname {sen}\theta ,\rho \cos \phi )\rho ^{2}\operatorname {sen}\phi \ d\rho \ d\phi \ d\theta$

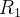onde $R_{1}$ é uma região do espaço- $\rho \phi \theta ,$ onde a integral em coordenadas esféricas se torna mais simples.

Ache o volume do sólido acima do cone $z^{2}=x^{2}+y^{2}$ e interior à esfera $x^{2}+y^{2}+z^{2}=4z.$

Solução: $\$ Em coordenadas esféricas temos

$\rho ^{2}=4\rho \cos \phi \text { ou }\rho =4\cos \phi \ \text {(Esfera de raio 2 centrada no ponto }\left( 0,0,2\right) \text {)}$

$\phi =\frac{\pi }{4}\ \ \text {(cone)}$

Logo o volume do sólido é

$V={\displaystyle \iiint _{S}} dV=\int _{0}^{2\pi }\int _{0}^{\frac{\pi }{4}}\int _{0}^{4\cos \phi }\rho ^{2}\operatorname {sen}\phi d\rho d\phi d\theta =8\pi .$

Ache o volume do sólido delimitado pelo cone $z=\sqrt{x^{2}+y^{2}}$ , pelo cilindro $x^{2}+y^{2}=4$ e pelo plano-xy. Ache o centróide.

Solução: O cilindro em coordenadas esféricas é

$\rho ^{2}\operatorname {sen}^{2}\phi =4\Rightarrow \rho =2/\operatorname {sen}\phi$

e o cone é

$\phi =\frac{\pi }{4}.$

Logo, o volume do sólido é

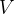	$\displaystyle V$	$\displaystyle =\int _{0}^{2\pi }\int _{\frac{\pi }{4}}^{\frac{\pi }{2}}\int _{0}^{2/\operatorname {sen}\phi }\rho ^{2}\operatorname {sen}\phi \ d\rho \ d\phi \ d\theta$
	$\displaystyle$	$\displaystyle =\int _{0}^{2\pi }\int _{\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{8}{3}\frac{1}{\operatorname {sen}^{2}\phi }\ d\phi \ d\theta$
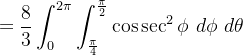	$\displaystyle$	$\displaystyle =\frac{8}{3}\int _{0}^{2\pi }\int _{\frac{\pi }{4}}^{\frac{\pi }{2}}\cos \sec ^{2}\phi \ d\phi \ d\theta$
	$\displaystyle$	$\displaystyle =\frac{8}{3}\int _{0}^{2\pi }-\cot \tan \phi \|_{\frac{\pi }{4}}^{\frac{\pi }{2}}d\theta$
	$\displaystyle$	$\displaystyle =\frac{16}{3}\pi$

Para encontrar o centróide, basta calcular o $\overline{z},$ isto é, só precisamos calcular o $M_{xy}:$

$M_{xy}={\displaystyle \iiint _{Q}} zdV=\int _{0}^{2\pi }\int _{\frac{\pi }{4}}^{\frac{\pi }{2}}\int _{0}^{2/\operatorname {sen}\phi }\rho \cos \phi \ \rho ^{2}\operatorname {sen}\phi \ d\rho \ d\phi \ d\theta =4\pi$

Logo,

$\overline{z}=\frac{M_{xy}}{V}=\frac{3}{4}.$

Ache o volume do sólido acima do cone $z=\sqrt{x^{2}+y^{2}}$ e interior à esfera $x^{2}+y^{2}+z^{2}=4z.$

Solução: Usando coordenadas esféricas temos que a equação da esfera de raio 2 e centrada no ponto $\left( 0,0,2\right)$ é

$\rho ^{2}=4\rho \cos \phi \text { ou \ }\rho =4\cos \phi$

e a do cone é

$\phi =\frac{\pi }{4}.$

O volume do sólido é

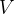	$\displaystyle V$	$\displaystyle ={\displaystyle \iiint _{Q}} dV=\int _{0}^{2\pi }\int _{0}^{\frac{\pi }{4}}\int _{0}^{4\cos \phi }\rho ^{2}\operatorname {sen}\phi \ d\rho \ d\phi \ d\theta$
	$\displaystyle$	$\displaystyle =2\pi \int _{0}^{\frac{\pi }{4}}\left[ \frac{\rho ^{3}}{3}\right] _{0}^{4\cos \phi }\operatorname {sen}\phi \ d\phi$
	$\displaystyle$	$\displaystyle =2\pi \int _{0}^{\frac{\pi }{4}}\frac{4^{3}}{3}\cos ^{3}\phi \operatorname {sen}\phi \ d\phi$
	$\displaystyle$	$\displaystyle =\frac{2.4^{2}.\pi }{3}\left[ -\cos ^{4}\phi \right] _{0}^{\frac{\pi }{4}}=\frac{2.4^{2}.\pi }{3}\left[ -\left[ \frac{\sqrt{2}}{2}\right] ^{4}+1\right]$
	$\displaystyle$	$\displaystyle =8\pi$

Em coordenadas cil $\'{\i }$ ndricas temos

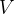	$\displaystyle V$	$\displaystyle ={\displaystyle \iint _{R}} \left[ \int _{\sqrt{x^{2}+y^{2}}}^{2+\sqrt{4-x^{2}-y^{2}}}dz\right] dA=\int _{0}^{2\pi }\int _{0}^{2}\int _{r}^{2+\sqrt{4-r^{2}}}r\ dz\ dr\ d\theta$
	$\displaystyle$	$\displaystyle =2\pi \int _{0}^{2}r\left[ 2+\sqrt{4-r^{2}}-r\right] dr=2\pi \int _{0}^{2}\left( 2r+r\sqrt{4-r^{2}}-r^{2}\right) dr$
	$\displaystyle$	$\displaystyle =2\pi \left[ r^{2}-\frac{r^{3}}{3}\right] _{0}^{2}+2\pi \int _{0}^{2}r\sqrt{4-r^{2}}dr=2\pi \left[ 4-\frac{8}{3}\right] -\frac{2\pi }{3}\left[ 4-r^{2}\right] ^{3/2}\|_{0}^{2}$
	$\displaystyle$	$\displaystyle =8\pi .$

Se esse sólido tiver densidade uniforme qual o seu centróide?

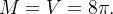
Solução: Basta calcular $\overline{z}=\frac{M_{xy}}{M},$ onde $M=V=8\pi .$

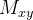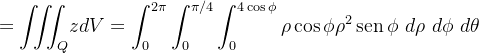	$\displaystyle M_{xy}$	$\displaystyle ={\displaystyle \iiint _{Q}} zdV=\int _{0}^{2\pi }\int _{0}^{\pi /4}\int _{0}^{4\cos \phi }\rho \cos \phi \rho ^{2}\operatorname {sen}\phi \ d\rho \ d\phi \ d\theta$
	$\displaystyle$	$\displaystyle =2\pi \int _{0}^{\pi /4}\cos \phi \operatorname {sen}\phi \left[ \frac{\rho ^{4}}{4}\right] _{0}^{4\cos \phi }d\phi =\frac{2.4^{4}.\pi }{4}\int _{0}^{\pi /4}\cos ^{5}\phi \operatorname {sen}\phi \ d\phi$
	$\displaystyle$	$\displaystyle =2.4^{3}.\pi \left[ -\frac{\cos ^{6}\phi }{6}\right] _{0}^{\pi /4}=\frac{4^{3}\pi }{3}\left[ -\left( \frac{\sqrt{2}}{2}\right) ^{6}+1\right]$
	$\displaystyle$	$\displaystyle =\frac{4^{3}\pi 7}{3.2.4}=\frac{56\pi }{3}.$

Logo,

$\overline{z}=\frac{56\pi }{3.8\pi }=\frac{7}{3}.$

Portanto, o centróide é: 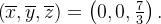$\left( \overline{x},\overline{y},\overline{z}\right) =\left( 0,0,\frac{7}{3}\right) .$

Calcule em coordenadas esféricas a integral

$\int _{-2}^{2}\int _{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}}}\int _{\sqrt{x^{2}+y^{2}}}^{\sqrt{8-x^{2}-y^{2}}}\left( x^{2}+y^{2}+z^{2}\right) \ dz\ dy\ dx.$

Solução: Temos que

	$\displaystyle \int _{-2}^{2}\int _{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}}}\int _{\sqrt{x^{2}+y^{2}}}^{\sqrt{8-x^{2}-y^{2}}}\left( x^{2}+y^{2}+z^{2}\right) \ dz\ dy\ dx$	$\displaystyle =\int _{0}^{2\pi }\int _{0}^{\pi /2}\int _{4/\cos \phi }^{8}\rho ^{2}\rho ^{2}\operatorname {sen}\phi \ d\rho \ d\phi \ d\theta$
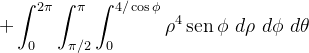	$\displaystyle$	$\displaystyle +\int _{0}^{2\pi }\int _{\pi /2}^{\pi }\int _{0}^{4/\cos \phi }\rho ^{4}\operatorname {sen}\phi \ d\rho \ d\phi \ d\theta$