| Cálculo Diferencial e Integral 3 |
Uma função que associa a cada valor real, um vetor, é chamada uma função com valor vetorial. Denotaremos tais funções por  ou
ou 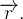
![\[ \mathbf{r}:X\rightarrow Y=\left\{ \text {conjunto de vetores do plano ou do espaço}\right\} ,\ \ X\subset \mathbb {R}\text {.} \]](images/img-0499.png) |
Se  é uma função vetorial, então para cada
é uma função vetorial, então para cada  em
em 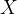
 existe um único vetor
existe um único vetor 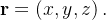 Como para cada
Como para cada  existe um valor
existe um valor  associado a ele, então
associado a ele, então 
 e
e  onde
onde  e
e  estão definidas em
estão definidas em 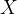 com valores reais. Logo podemos escrever
com valores reais. Logo podemos escrever
 |
(1) |
para todo  em
em 
A recíproca é verdadeira, se  e
e  são funções de
são funções de 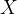 em
em 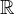 , então podemos definir uma função vetorial
, então podemos definir uma função vetorial  por meio de
por meio de  .
.  é uma função vetorial se, e somente se,
é uma função vetorial se, e somente se,  puder ser expressa na forma
puder ser expressa na forma  O domínio de
O domínio de  é a interseção dos domínios de
é a interseção dos domínios de  e
e 
Se 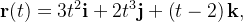 determine
determine 
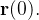
Solução:
![\[ \mathbf{r}(1)=3\mathbf{i}+2\mathbf{j}-\mathbf{k,\ \ r}(0)=-2\mathbf{k.} \]](images/img-0520.png) |
Uma curva no espaço é um conjunto 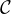 de ternos ordenados da forma
de ternos ordenados da forma
![\[ (f(t),g(t),h(t)) \]](images/img-0522.png) |
onde as funções  e
e  são contínuas num intervalo
são contínuas num intervalo  da reta
da reta O gráfico de
O gráfico de 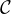 num sistema de coordenadas retangulares é o conjunto de todos os pontos
num sistema de coordenadas retangulares é o conjunto de todos os pontos  que correspondem aos ternos ordenados em
que correspondem aos ternos ordenados em 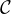 . As equações
. As equações
 |
(2) |
onde  pertence a
pertence a  são as equações paramétricas de
são as equações paramétricas de 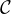 . Se
. Se ![$I=[a,b]$](images/img-0527.png) e
e 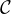 não se auto intercepta, exceto possivelmente, no ponto
não se auto intercepta, exceto possivelmente, no ponto  então pode-se mostrar que o comprimento
então pode-se mostrar que o comprimento 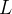 de
de 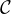 do ponto
do ponto 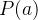 ao ponto
ao ponto  é dado por
é dado por
 |
(3) |
Considere uma função vetorial 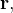 onde
onde 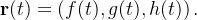 O gráfico de
O gráfico de  pode ser descrito na figura abaixo.
pode ser descrito na figura abaixo.
Seja 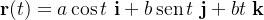 ,
,  , e seja
, e seja  o vetor posição de
o vetor posição de 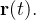
(a) Esboce o gráfico da curva 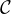 descrita por
descrita por 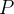 ao variar
ao variar 
(b) Determine o comprimento de 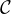 entre os pontos correspondentes a
entre os pontos correspondentes a  e
e 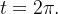
Solução: O gráfico da curva 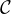 é dado pela figura.
é dado pela figura.
(b) O comprimento de 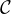 entre os pontos correspondentes a
entre os pontos correspondentes a  e
e  é calculado por
é calculado por
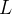 |
 |
|||
 |
 |