5.1 Integral em coordenadas esféricas

Considerando um elemento esférico temos que

$\left\Vert PR\right\Vert =\rho _{k}\Delta \phi _{k},\ \left\Vert RS\right\Vert =\left\Vert RP^{\prime }\right\Vert \Delta \theta _{k},\ \left\Vert RP^{\prime }\right\Vert =\rho _{k}\operatorname {sen}\phi _{k},\ \left\Vert PT\right\Vert =\Delta \rho _{k}$

assim

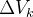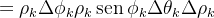	$\displaystyle \Delta V_{k}$	$\displaystyle =\rho _{k}\Delta \phi _{k}\rho _{k}\operatorname {sen}\phi _{k}\Delta \theta _{k}\Delta \rho _{k}$
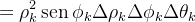	$\displaystyle$	$\displaystyle =\rho _{k}^{2}\operatorname {sen}\phi _{k}\Delta \rho _{k}\Delta \phi _{k}\Delta \theta _{k}$

formamos a soma de Riemann

$\sum _{k}f(r_{k},\phi _{k},\theta _{k})\Delta V_{k}$

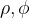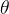da $\'{\i }$ concluimos que: se supomos $f$ uma função de $\rho ,\phi$ e $\theta$ cont $\'{\i }$ nua numa região da forma

$Q=\left\{ \left( \rho ,\phi ,\theta \right) ;\ a\leq \rho \leq b,\ c\leq \phi \leq d,\ m\leq \theta \leq n\right\}$

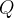a integral de $f$ sobre $Q$ é

${\displaystyle \iiint _{Q}} f(r,\phi ,\theta )dV=\int _{m}^{n}\int _{c}^{d}\int _{a}^{b}f(\rho ,\phi ,\theta )\rho ^{2}\operatorname {sen}\phi d\rho \ d\phi \ d\theta .$

Ache o centróide de um sólido hemisférico 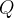$Q$ de raio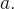 $a.$

Solução: Basta achar 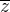$\overline{z}$ , temos

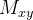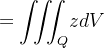	$\displaystyle M_{xy}$	$\displaystyle ={\displaystyle \iiint _{Q}} zdV$
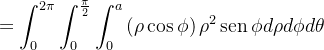	$\displaystyle$	$\displaystyle =\int _{0}^{2\pi }\int _{0}^{\frac{\pi }{2}}\int _{0}^{a}\left( \rho \cos \phi \right) \rho ^{2}\operatorname {sen}\phi d\rho d\phi d\theta$
	$\displaystyle$	$\displaystyle =\int _{0}^{2\pi }\int _{0}^{\frac{\pi }{2}}\left[ \frac{\rho ^{4}}{4}\right] _{0}^{a}\operatorname {sen}\phi \cos \phi d\phi d\theta$
	$\displaystyle$	$\displaystyle =\frac{a^{4}}{4}\int _{0}^{2\pi }\int _{0}^{\frac{\pi }{2}}\left[ \frac{\operatorname {sen}^{2}\phi }{2}\right] _{0}^{\frac{\pi }{2}}d\theta$
	$\displaystyle$	$\displaystyle =\frac{a^{4}}{8}\left[ \theta \right] _{0}^{2\pi }=\frac{1}{4}\pi a^{4}.$

Logo,

$\overline{z}=\frac{M_{xy}}{V}=\frac{\frac{1}{4}\pi a^{4}}{\frac{2}{3}\pi a^{3}}=\frac{3}{8}a.$