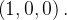| Cálculo Diferencial e Integral 3 |
Seja 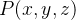 um ponto situado no espaço. Podemos considerar esse ponto situado em coordenadas esféricas como segue. Se
um ponto situado no espaço. Podemos considerar esse ponto situado em coordenadas esféricas como segue. Se 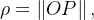 seja
seja  o ângulo entre
o ângulo entre 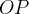 e o vetor
e o vetor 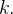 A projeção desse ponto no eixo-z determinamos o ponto
A projeção desse ponto no eixo-z determinamos o ponto 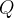 , e consideramos o vetor
, e consideramos o vetor 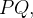 quando projetamos o ponto
quando projetamos o ponto 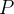 no plano-xy temos o ponto
no plano-xy temos o ponto 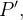 então claramente, temos que
então claramente, temos que  e podemos escrever
e podemos escrever 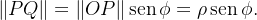 Temos também que
Temos também que 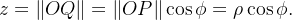 Desse modo, temos que
Desse modo, temos que 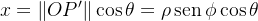 e
e 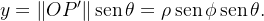 Assim as coordenadas cartesianas do ponto
Assim as coordenadas cartesianas do ponto 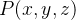 são transformadas para as coordenadas
são transformadas para as coordenadas
![\[ x=\rho \operatorname {sen}\phi \cos \theta ,\ y=\rho \operatorname {sen}\phi \operatorname {sen}\theta ,\ \ z=\rho \cos \phi ; \]](images/img-0407.png) |
estas são as coordenadas esféricas do ponto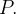 Note que a variação de
Note que a variação de  e
e  são dadas da seguinte forma
são dadas da seguinte forma
![\[ \rho \geq 0,\ \ 0\leq \phi \leq \pi ,\ 0\leq \theta \leq 2\pi . \]](images/img-0410.png) |
Se 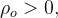 o gráfico de
o gráfico de 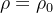 é uma esfera de raio
é uma esfera de raio 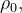 com centro na origem
com centro na origem 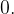 Se
Se 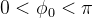 então o gráfico de
então o gráfico de 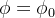 é um meio cone de vértice na origem
é um meio cone de vértice na origem 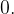 O gráfico de
O gráfico de 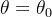 é um semiplano contendo o eixo-z.
é um semiplano contendo o eixo-z.
Se um ponto 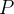 tem coordenadas esféricas
tem coordenadas esféricas 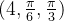 , ache as coordenadas retangulares e cilindricas de
, ache as coordenadas retangulares e cilindricas de 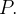
Solução: Temos que 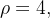
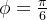 e
e 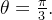 Então
Então
![\[ x=4\operatorname {sen}\frac{\pi }{6}\cos \frac{\pi }{3}=4\left( \frac{1}{2}\right) \left( \frac{1}{2}\right) =1 \]](images/img-0421.png) |
![\[ y=4\operatorname {sen}\frac{\pi }{6}\operatorname {sen}\frac{\pi }{3}=4\left( \frac{1}{2}\right) \left( \frac{\sqrt{3}}{2}\right) =\sqrt{3} \]](images/img-0422.png) |
![\[ z=4\cos \frac{\pi }{6}=4\left( \frac{\sqrt{3}}{2}\right) =2\sqrt{3} \]](images/img-0423.png) |
Para achar as coordenadas cilindricas de 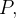 temos que
temos que
![\[ r^{2}=x^{2}+y^{2}=1+3=4 \]](images/img-0424.png) |
e então 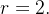 Assim as coordenadas cilindricas de
Assim as coordenadas cilindricas de 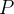 são
são 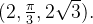
Ache uma equação em coordenadas esféricas cujo gráfico seja o parabolóide 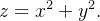
Solução: Temos que
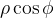 |
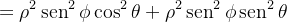 |
|||
 |
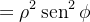 |
ou
![\[ \rho \left( \cos \phi -\rho \operatorname {sen}^{2}\phi \right) =0 \]](images/img-0431.png) |
segue que
![\[ \rho \operatorname {sen}^{2}\phi =\cos \phi \]](images/img-0432.png) |
ou
![\[ \rho =\frac{\cos \phi }{\operatorname {sen}^{2}\phi } \]](images/img-0433.png) |
ou ainda
![\[ \rho =\cot \phi \cos \sec \phi . \]](images/img-0434.png) |
Transforme a equação 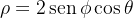 para coordenadas retangulares e descreva seu gráfico.
para coordenadas retangulares e descreva seu gráfico.
Solução:  Temos que
Temos que
![\[ \rho ^{2}=2\rho \operatorname {sen}\phi \cos \theta \]](images/img-0436.png) |
ou
![\[ x^{2}+y^{2}+z^{2}=2x \]](images/img-0437.png) |
ou ainda
![\[ \left( x-1\right) ^{2}+y^{2}+z^{2}=1. \]](images/img-0438.png) |
Logo essa é a equação da esfera de raio 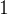 centrada no ponto
centrada no ponto