| Cálculo Diferencial e Integral 3 |
Suponha 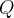 uma região do tipo
uma região do tipo
![\[ Q=\left\{ \left( r,\theta ,z\right) ;\ a\leq r\leq b,\ c\leq \theta \leq d,\ m\leq z\leq n\right\} \]](images/img-0347.png) |
e  uma função cont
uma função cont nua dependente de
nua dependente de 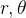 e
e  em
em 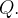 Então
Então
![\[ {\displaystyle \iiint _{Q}} f(r,\theta ,z)dV=\int _{m}^{n}\int _{c}^{d}\int _{a}^{b}f(r,\theta ,z)rdrd\theta dz. \]](images/img-0349.png) |
Suponha agora que 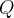 é do tipo
é do tipo
![\[ Q=\left\{ \left( r,\theta ,z\right) ;\left( r,\theta \right) \in R\text { e }k_{1}(r,\theta )\leq z\leq k_{2}\left( r,\theta \right) \right\} \]](images/img-0350.png) |
onde  é uma região do tipo
é uma região do tipo
![\[ R=\left\{ \left( r,\theta \right) ;\alpha \leq \theta \leq \beta ,\ \ g_{1}(\theta )\leq r\leq g_{2}(\theta )\right\} \]](images/img-0351.png) |
então temos que
![\[ {\displaystyle \iiint _{Q}} f(r,\theta ,z)dV={\displaystyle \iint _{R}} \left[ \int _{k_{1}(r,\theta )}^{k_{2}\left( r,\theta \right) }f(r,\theta ,z)\ dz\right] dA \]](images/img-0352.png) |
que pode ser escrita como
![\[ {\displaystyle \iiint _{Q}} f(r,\theta ,z)dV=\int _{\alpha }^{\beta }\int _{g_{1}\left( \theta \right) }^{g_{2}\left( \theta \right) }\int _{k_{1}(r,\theta )}^{k_{2}\left( r,\theta \right) }f(r,\theta ,z)\ dzdrd\theta \]](images/img-0353.png) |
Ache o centróide de um sólido hemisférico 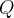 de raio
de raio 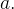
Solução: Temos que
![\[ x^{2}+y^{2}+z^{2}=a^{2} \]](images/img-0354.png) |
logo, a massa desse sólido é calculada como
![\[ m={\displaystyle \iiint _{Q}} dV=\int _{0}^{2\pi }\int _{0}^{a}\int _{0}^{\sqrt{a^{2}-r^{2}}}dzrdrd\theta =\frac{2\pi }{3}a^{3}. \]](images/img-0355.png) |
Por simetria o centróide está sobre o eixo-z, então basta achar o 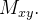 Como
Como
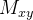 |
![$\displaystyle ={\displaystyle \iiint _{Q}} zdV=\int _{0}^{2\pi }\int _{0}^{a}\int _{0}^{\sqrt{a^{2}-r^{2}}}zdzrdrd\theta =\int _{0}^{2\pi }\int _{0}^{a}\left[ \frac{z^{2}}{2}\right] _{0}^{\sqrt{a^{2}-r^{2}}}rdrd\theta $](images/img-0357.png) |
|||
 |
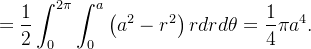 |
Logo
![\[ \overline{z}=\frac{3}{8}a. \]](images/img-0359.png) |
Um sólido  é delimitado pelo cone
é delimitado pelo cone  e pelo plano
e pelo plano  A densidade em cada ponto
A densidade em cada ponto  do cone é diretamente proporcional à distância da origem a
do cone é diretamente proporcional à distância da origem a  Ache sua massa.
Ache sua massa.
Solução: Temos que
![\[ \delta \left( x,y,z\right) =k\left( r^{2}+z^{2}\right) \]](images/img-0363.png) |
Logo
![\[ m=\int _{0}^{2\pi }\int _{0}^{2}\int _{r}^{2}k(r^{2}+z^{2})rdzdrd\theta . \]](images/img-0364.png) |
Suponha uma região  no espaço, cuja projeção no plano-
no espaço, cuja projeção no plano- seja uma região
seja uma região  , descrita em coordenadas polares. Isto é,
, descrita em coordenadas polares. Isto é,
![\[ G=\left\{ \left( x,y,z\right) \in \mathbb {R}^{3};\; \left( x,y\right) \in D\text { e }g_{1}(x,y)\leq z\leq g_{2}(x,y)\right\} \]](images/img-0367.png) |
e
![\[ D=\left\{ (r,\theta )\in \mathbb {R}^{2};\; \alpha \leq \theta \leq \beta ,\; 0\leq h_{1}(\theta )\leq r\leq h_{2}(\theta )\right\} . \]](images/img-0368.png) |
Nesse caso, temos
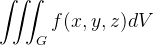 |
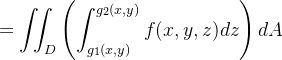 |
|||
 |
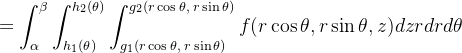 |
Este é o teorema de mudança de variável das coordenadas cartesianas para coordenadas cilindricas.
Calcule o centróide da parte da esfera 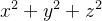
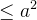 (
(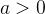 ) que está no primeiro octante.
) que está no primeiro octante.
Sol.: A reta 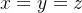 é a reta de simetria da parte da esfera. De modo que o centróide pertence a esta reta. Assim temos
é a reta de simetria da parte da esfera. De modo que o centróide pertence a esta reta. Assim temos 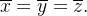 Calculando
Calculando  temos
temos
![\[ V\overline{z}=\iiint _{G}zdV \]](images/img-0378.png) |
onde  é o volume da parte da esfera representada por
é o volume da parte da esfera representada por  Usando coordenadas cil
Usando coordenadas cil ndricas, fazemos a substituição
ndricas, fazemos a substituição 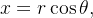
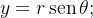 os limites de integração de
os limites de integração de  , ficam
, ficam  a
a  Portanto:
Portanto:
![\[ \iiint _{G}zdV=\iint _{D}\left( \int _{0}^{\sqrt{a^{2}-r^{2}}}zdz\right) dA=\iint _{D}\frac{1}{2}(a^{2}-r^{2})dA \]](images/img-0383.png) |
onde 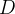 é o quarto de c
é o quarto de c rculo de raio
rculo de raio 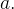 Agora calculando a integral dupla usando coordenadas polares temos:
Agora calculando a integral dupla usando coordenadas polares temos:
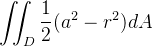 |
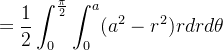 |
|||
 |
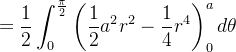 |
|||
 |
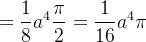 |
Portanto,
![\[ \iiint _{G}zdV=\frac{1}{16}a^{4}\pi \]](images/img-0388.png) |
Agora como 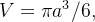 resulta que
resulta que
![\[ \overline{z}=\frac{3a}{8}=\overline{x}=\overline{y}. \]](images/img-0390.png) |
Transformar para coordenadas cil ndricas a integral abaixo:
ndricas a integral abaixo:
![\[ \iiint _{R}x^{2}ydxdydz, \]](images/img-0391.png) |
 é dada por
é dada por 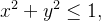
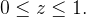
Sol.:
![\[ \int _{0}^{2\pi }\int _{0}^{1}\int _{0}^{1}r^{4}\cos ^{2}\theta \sin \theta dzdrd\theta . \]](images/img-0394.png) |
Transformar para coordenadas cil ndricas a integral abaixo
ndricas a integral abaixo
![\[ \int _{0}^{1}\int _{0}^{\sqrt{1-x^{2}}}\int _{0}^{1+x+y}(x^{2}-y^{2})dzdydx. \]](images/img-0395.png) |
Sol.:
![\[ \int _{0}^{\frac{\pi }{2}}\int _{0}^{1}\int _{0}^{1+r(\cos \theta +\sin \theta )}r^{3}\cos 2\theta dzdrd\theta . \]](images/img-0396.png) |