| Cálculo Diferencial e Integral 3 |
Considere a região  como na figura 1, delimitada por arcos de c
como na figura 1, delimitada por arcos de c rculos de raios
rculos de raios 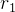 e
e 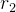 e por dois raios que saem da origem. Se
e por dois raios que saem da origem. Se 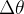 é a medida em radianos do ângulo entre os raios e se
é a medida em radianos do ângulo entre os raios e se 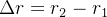 então a área
então a área 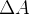 de
de  é
é
![\[ \Delta A=\frac{1}{2}r_{2}^{2}\Delta \theta -\frac{1}{2}r_{1}^{2}\Delta \theta \]](images/img-0141.png) |
ou
![\[ \Delta A=\frac{1}{2}(r_{2}^{2}-r_{1}^{2})\Delta \theta =\frac{1}{2}(r_{2}+r_{1})(r_{2}-r_{1})\Delta \theta \]](images/img-0142.png) |
chamando 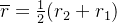 então
então
![\[ \Delta A=\overline{r}\Delta r\Delta \theta . \]](images/img-0144.png) |
Agora consideremos a região  como na figura 2, delimitada por dois raios que fazem ângulos
como na figura 2, delimitada por dois raios que fazem ângulos 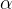 e
e 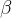 com o eixo polar, e pelos gráficos de suas equações polares
com o eixo polar, e pelos gráficos de suas equações polares 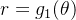 e
e 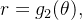 em que
em que 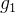 e
e 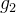 são funções cont
são funções cont nuas e
nuas e 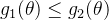 para
para 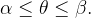
Subdividimos  por meio de arcos circulares e raios conforme a figura 2. Então a coleção de regiões polares elementares
por meio de arcos circulares e raios conforme a figura 2. Então a coleção de regiões polares elementares  que estão completamente dentro de
que estão completamente dentro de  é chamada a partição polar interior
é chamada a partição polar interior 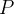 de
de 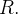 A
A  é o comprimento da maior diagonal dos
é o comprimento da maior diagonal dos 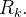 Escolhido um ponto
Escolhido um ponto  em
em 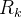 talque
talque 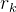 seja o raio médio, então
seja o raio médio, então
![\[ \Delta A_{k}=r_{k}\Delta r_{k}\Delta \theta _{k}. \]](images/img-0158.png) |
Se  é uma função cont
é uma função cont nua das variáveis polares
nua das variáveis polares  e
e 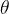 então temos o seguinte resultado.
então temos o seguinte resultado.
![\[ \iint _{R}f(r,\theta )dA=\int _{\alpha }^{\beta }\int _{g_{1}(\theta )}^{g_{2}(\theta )}f(r,\theta )rdrd\theta \]](images/img-0161.png) |
![\[ =\lim _{\left\| P\right\| \rightarrow 0}\sum _{k}f(r_{k},\theta _{k})r_{k}\Delta r_{k}\Delta \theta _{k}. \]](images/img-0162.png) |
Se 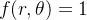 em toda
em toda 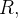 então a integral acima é igual a área de
então a integral acima é igual a área de 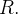
Ache a área da região  exterior ao c
exterior ao c rculo
rculo  e interior ao c
e interior ao c rculo
rculo 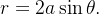
Sol.: Os pontos de interseção destes c rculos são:
rculos são:
![\[ a=2a\sin \theta \Rightarrow \sin \theta =\frac{1}{2}\Rightarrow \theta _{1}=\frac{\pi }{6}\text { e }\theta _{2}=\frac{5\pi }{6}. \]](images/img-0166.png) |
Logo:
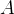 |
![$\displaystyle =\int _{\frac{\pi }{6}}^{\frac{5\pi }{6}}\int _{a}^{2a\sin \theta }rdrd\theta =\int _{\frac{\pi }{6}}^{\frac{5\pi }{6}}[\frac{r^{2}}{2}]_{a}^{2a\sin \theta }d\theta = $](images/img-0167.png) |
|||
 |
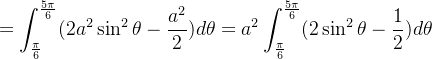 |
|||
 |
![$\displaystyle =a^{2}\int _{\frac{\pi }{6}}^{\frac{5\pi }{6}}(1-\cos 2\theta -\frac{1}{2})d\theta =a^{2}[\frac{1}{2}\theta -\frac{\sin 2\theta }{2}]_{\frac{\pi }{6}}^{\frac{5\pi }{6}} $](images/img-0169.png) |
|||
 |
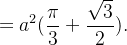 |
Note que 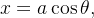
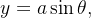 nos faz deduzir que
nos faz deduzir que
![\[ r=2a\sin \theta \]](images/img-0173.png) |
implica em
![\[ x^{2}+y^{2}=2ay\Rightarrow x^{2}+y^{2}-2ay+a^{2}=a^{2}\Rightarrow x^{2}+(y-a)^{2}=a^{2}. \]](images/img-0174.png) |
Ache a área da região  delimitada pelo laço da lemniscata
delimitada pelo laço da lemniscata 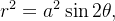
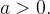
Sol.: Quando 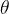 variar de
variar de 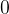 a
a 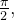 varremos um laço da lemniscata. Segue que:
varremos um laço da lemniscata. Segue que:
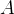 |
![$\displaystyle =\int _{0}^{\frac{\pi }{2}}\int _{0}^{\sqrt{a^{2}\sin 2\theta }}rdrd\theta =\int _{0}^{\frac{\pi }{2}}[\frac{r^{2}}{2}]_{0}^{a\sqrt{\sin 2\theta }}d\theta $](images/img-0178.png) |
|||
 |
![$\displaystyle =\frac{1}{2}\int _{0}^{\frac{\pi }{2}}a^{2}\sin 2\theta d\theta =-\frac{1}{4}a^{2}[\cos 2\theta ]_{0}^{\frac{\pi }{2}} $](images/img-0179.png) |
|||
 |
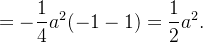 |
Fórmula de mudança de variável:
![\[ \iint _{R}f(x,y)dydx=\iint f(r\cos \theta ,r\sin \theta )rdrd\theta . \]](images/img-0181.png) |
Utilize coordenadas polares para calcular
![\[ \int _{-a}^{a}\int _{0}^{\sqrt{a^{2}-x^{2}}}(x^{2}+y^{2})^{\frac{3}{2}}dydx. \]](images/img-0182.png) |