| Cálculo Diferencial e Integral 3 |
Já vimos que se 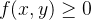 e
e  é cont
é cont nua, então o volume
nua, então o volume  do sólido compreendido entre o gráfico de
do sólido compreendido entre o gráfico de 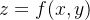 e sobre uma região
e sobre uma região 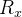 do plano
do plano  é:
é:
![\[ V=\iint _{R}f(x,y)dA \]](images/img-0096.png) |
Deduz-se portanto, que
![\[ V=\int _{a}^{b}\int _{g_{1}(x)}^{g_{2}(x)}f(x,y)dydx. \]](images/img-0097.png) |
A área da região 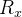 é dada por:
é dada por:
![\[ A=\iint _{R_{x}}dA \]](images/img-0098.png) |
neste caso,
![\[ A=\int _{a}^{b}\int _{g_{1}(x)}^{g_{2}(x)}dydx=\int _{a}^{b}[y]_{g_{1}(x)}^{g_{2}(x)}dx=\int _{a}^{b}[g_{2}(x)-g_{1}(x)]dx. \]](images/img-0099.png) |
Analogamente, para 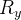 é verdade.
é verdade.
Ache a área 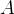 da região do plano-
da região do plano- delimitada pelos gráficos de
delimitada pelos gráficos de 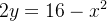 e
e 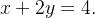
Sol.: Temos que
![\[ y=8-\frac{x^{2}}{2}\text { e }y=2-\frac{x}{2}. \]](images/img-0104.png) |
Interceptando as duas equações acima obtemos
![\[ 2-\frac{x}{2}=8-\frac{x^{2}}{2}\text { \ \ ou }2-\frac{x}{2}=2(4-\frac{x^{2}}{4})\text {\ \ } \]](images/img-0105.png) |
ou ainda
![\[ 2-\frac{x}{2}=2(2-\frac{x}{2})(2+\frac{x}{2})\text { \ ou \ }(2-\frac{x}{2})[1-2(2+\frac{x}{2})]=0\text { } \]](images/img-0106.png) |
o que implica
![\[ (2-\frac{x}{2})(-3-x)=0\Rightarrow \left\{ \begin{array}[c]{c}x=-3,\text { ou}\\ x=4 \end{array} \right. . \]](images/img-0107.png) |
Logo:
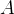 |
![$\displaystyle =\int _{-3}^{4}\int _{2-\frac{x}{2}}^{8-\frac{x^{2}}{2}}dydx=\int _{-3}^{4}[8-\frac{x^{2}}{2}-(2-\frac{x}{2})]dx=\int _{-3}^{4}[6+\frac{x}{2}-\frac{x^{2}}{2}]dx $](images/img-0109.png) |
|||
 |
![$\displaystyle =[6x+\frac{x^{2}}{4}-\frac{x^{3}}{6}]_{-3}^{4}=\frac{343}{12}. $](images/img-0110.png) |
Ache a área 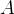 da região do plano-
da região do plano- delimitada pelos gráficos de
delimitada pelos gráficos de 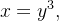
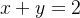 e
e 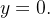
Sol.: Interceptando 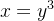 com
com 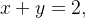 obtemos:
obtemos:
![\[ y^{3}+y-2=0 \]](images/img-0116.png) |
cuja raiz é 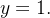 Logo, temos:
Logo, temos:
![\[ A=\int _{0}^{1}\int _{y^{3}}^{2-y}dxdy=\int _{0}^{1}[x]_{y^{3}}^{2-y}dy=\int _{0}^{1}(2-y-y^{3})dy=[2y-\frac{y^{2}}{2}-\frac{y^{4}}{4}]_{0}^{1}=\frac{5}{4}. \]](images/img-0118.png) |
Ou:
![\[ A=\int _{0}^{1}\int _{0}^{\sqrt[3]{x}}dydx+\int _{1}^{2}\int _{0}^{2-x}dydx. \]](images/img-0119.png) |
Ache o volume do sólido do primeiro octante delimitado pleos planos coordenados, pelo parabolóide 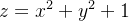 e pelo plano
e pelo plano 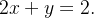
Sol.: Temos que
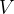 |
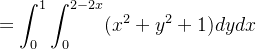 |
|||
 |
![$\displaystyle =\int _{0}^{1}[x^{2}y+\frac{y^{3}}{3}+y]_{0}^{2-2x}dx $](images/img-0124.png) |
|||
 |
![$\displaystyle =\int _{0}^{1}[x^{2}(2-2x)+\frac{(2-2x)^{3}}{3}+(2-2x)]dx $](images/img-0125.png) |
|||
 |
![$\displaystyle =\int _{0}^{1}[-\frac{14}{3}x^{3}+10x^{2}-10x+\frac{14}{3}]dx $](images/img-0126.png) |
|||
 |
![$\displaystyle =[-\frac{7}{6}x^{4}+\frac{10}{3}x^{3}-5x^{2}+\frac{14}{3}x]_{0}^{1}=\frac{11}{6}. $](images/img-0127.png) |
Ache o volume  do sólido que está no primeiro octante e é delimitado pelos três planos coordenados e pelos cilindros
do sólido que está no primeiro octante e é delimitado pelos três planos coordenados e pelos cilindros 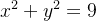 e
e 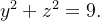
Sol.: O sólido está situado abaixo do gráfico de 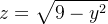 e acima da região
e acima da região  (que equivale a um quarto do c
(que equivale a um quarto do c rculo
rculo 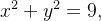 junto com os pontos interiores ao c
junto com os pontos interiores ao c rculo). Assim:
rculo). Assim:
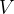 |
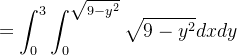 |
|||
 |
![$\displaystyle =\int _{0}^{3}\sqrt{9-y^{2}}[x]_{0}^{\sqrt{9-y^{2}}}dy $](images/img-0133.png) |
|||
 |
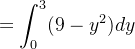 |
|||
 |
![$\displaystyle =[9y-\frac{y^{3}}{3}]_{0}^{3}=18. $](images/img-0135.png) |