| Cálculo Diferencial e Integral 3 |
Suponha que temos uma lâmina não-homogênea 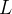 que tenha a forma de uma região
que tenha a forma de uma região  do plano-xy. Se a densidade de massa por área no ponto
do plano-xy. Se a densidade de massa por área no ponto 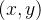 é
é 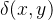 e
e 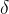 é cont
é cont nua em
nua em 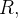 então
então
![\[ m=\iint _{R}\delta (x,y)dA \]](images/img-0186.png) |
Seja 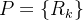 uma partição de
uma partição de  e, para cada
e, para cada 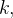 seja
seja 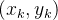 um ponto arbitrário de
um ponto arbitrário de 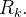 Como
Como 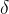 é cont
é cont nua, podemos pensar que
nua, podemos pensar que 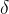 é quase constante em
é quase constante em 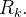 Logo, se
Logo, se 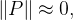 a massa
a massa 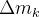 que corresponde a
que corresponde a 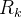 pode ser aproximada por
pode ser aproximada por 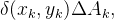 em que
em que 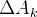 é a área de
é a área de 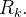 Admitindo a massa
Admitindo a massa 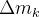 concentrada em
concentrada em  então o momento deste elemento de
então o momento deste elemento de 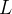 em relação ao eixo-x é o produto de
em relação ao eixo-x é o produto de 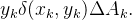 Como a soma dos momentos deve aproximar o momento da lâmina, definimos o momento
Como a soma dos momentos deve aproximar o momento da lâmina, definimos o momento 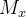 de
de 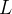 em relação ao eixo-x como segue:
em relação ao eixo-x como segue:
![\[ M_{x}=\lim _{\left\| P\right\| \rightarrow 0}\sum _{k}y_{k}\delta (x_{k},y_{k})\Delta A_{k}=\iint _{R}y\delta (x,y)dA \]](images/img-0197.png) |
Da mesma forma o momento 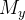 de
de 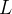 em relação ao eixo-y é
em relação ao eixo-y é
![\[ M_{y}=\lim _{\left\| P\right\| \rightarrow 0}\sum _{k}x_{k}\delta (x_{k},y_{k})\Delta A_{k}=\iint _{R}x\delta (x,y)dA \]](images/img-0199.png) |
Definimos o centro de massa (ou centro de gravidade) da lâmina como o ponto 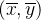 tal que
tal que 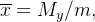

Se 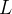 é homogênea, então a densidade de massa por área
é homogênea, então a densidade de massa por área 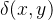 é constante e pode ser cancelada nas equações acima.
é constante e pode ser cancelada nas equações acima.
Uma lâmina tem a forma de um triângulo retângulo isósceles com lados iguais de comprimento 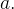 A densidade de massa por área no ponto
A densidade de massa por área no ponto 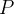 é diretamente proporcional ao quadrado da distância de
é diretamente proporcional ao quadrado da distância de 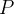 ao vértice oposto à hipotenusa. Ache o centro de massa.
ao vértice oposto à hipotenusa. Ache o centro de massa.
Sol.:
A lâmina é a mesma do exemplo anterior. Temos que 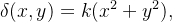 e já sabemos que
e já sabemos que 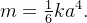 Por definição:
Por definição:
![\[ M_{y}=\iint _{R}xk(x^{2}+y^{2})dA=\int _{0}^{a}\int _{0}^{a-x}xk(x^{2}+y^{2})dydx=\frac{1}{15}ka^{5}. \]](images/img-0206.png) |
Logo,
![\[ \overline{x}=\frac{\frac{1}{15}ka^{5}}{\frac{1}{6}ka^{4}}=\frac{2}{5}a. \]](images/img-0207.png) |
Analogamente, 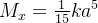 e
e 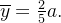 Assim, o centro de massa da lâmina é
Assim, o centro de massa da lâmina é 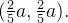
Uma lâmina tem a forma da região  do plano-
do plano- delimitada pela parábola
delimitada pela parábola 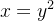 e a reta
e a reta 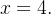 A densidade de massa por área no ponto
A densidade de massa por área no ponto 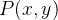 é diretamente proporcional à distância do eixo-
é diretamente proporcional à distância do eixo-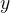 a
a 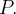 Ache o centro de massa.
Ache o centro de massa.
Sol.:
A densidade de massa por área em 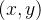 é
é 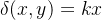 para uma constante
para uma constante 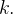 Segue-se da forma de
Segue-se da forma de 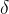 e da simetria da região, que o centro de massa está sobre o eixo-
e da simetria da região, que o centro de massa está sobre o eixo- , isto é,
, isto é, 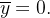
Por definição, temos que
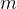 |
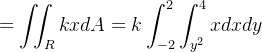 |
|||
 |
![$\displaystyle =k\int _{-2}^{2}\left[ \frac{1}{2}x^{2}\right] _{y^{2}}^{4}dy=\frac{1}{2}k\int _{-2}^{2}(16-y^{4})dy=\frac{128}{5}k. $](images/img-0220.png) |
Temos também que
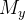 |
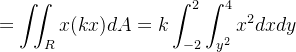 |
|||
 |
![$\displaystyle =k\int _{-2}^{2}\left[ \frac{1}{3}x^{3}\right] _{y^{2}}^{4}dy=\frac{1}{3}k\int _{-2}^{2}(64-y^{6})dy=\frac{512}{7}k. $](images/img-0223.png) |
Consequentemente:
![\[ \overline{x}=\frac{M_{y}}{m}=\frac{512k}{7}.\frac{5}{128k}=\frac{20}{7}, \]](images/img-0224.png) |
logo o centro de massa é 
Momentos de Inércia de uma lâmina:
![\[ I_{x}=\iint _{R}y^{2}\delta (x,y)dA\; \; \text {(Momento de In\'{e}rcia em rela\c{c}\~{a}o ao eixo-}x\text {)} \]](images/img-0226.png) |
![\[ I_{y}=\iint _{R}x^{2}\delta (x,y)dA\; \; \text {(Momento de In\'{e}rcia em rela\c{c}\~{a}o ao eixo-}y\text {)} \]](images/img-0227.png) |
![\[ I_{0}=\iint _{R}\left( x^{2}+y^{2}\right) \delta (x,y)dA\text { \ (Momento polar de In\'{e}rcia, em rela\c{c}\~{a}o \`{a} origem).} \]](images/img-0228.png) |
Uma lâmina tem a forma semicircular da figura *. A densidade de massa por área é diretamente proporcional à distância do eixo- . Ache o momento de inércia em relação ao eixo-
. Ache o momento de inércia em relação ao eixo-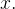
Sol.:
Por hipótese, a densidade de massa por área em 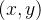 é
é 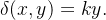 Temos que o momento de inércia em relação ao eixo-
Temos que o momento de inércia em relação ao eixo- é
é
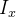 |
![$\displaystyle =\int _{-a}^{a}\int _{0}^{\sqrt{a^{2}-x^{2}}}y^{2}(ky)dydx=k\int _{-a}^{a}\left[ \frac{1}{4}y^{4}\right] _{0}^{\sqrt{a^{2}-x^{2}}}dx $](images/img-0232.png) |
|||
 |
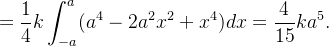 |
Os momentos de inércia são úteis em problemas que envolvem a rotação de um objeto em torno de um eixo fixo. Por exemplo, a rotação de uma roda ( ou um disco) em torno de um eixo. Se uma part cula
cula 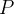 da roda tem massa
da roda tem massa 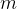 e está a uma distância
e está a uma distância 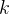 do eixo de rotação, então o momento de inércia
do eixo de rotação, então o momento de inércia  de
de 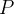 em relação ao eixo é
em relação ao eixo é 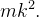 Se a velocidade angular
Se a velocidade angular 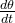 é uma constante
é uma constante 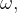 então a velocidade
então a velocidade 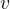 da part
da part cula é
cula é 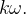 Sabemos que
Sabemos que
![\[ E_{c}=\frac{1}{2}mv^{2}. \]](images/img-0242.png) |
Como 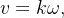
![\[ E_{c}=\frac{1}{2}mk^{2}w^{2}=\frac{1}{2}I\omega ^{2}. \]](images/img-0244.png) |
Como  a energia cinética é diretamente proporcional ao momento de inércia.
a energia cinética é diretamente proporcional ao momento de inércia.
Consideremos agora um sólido com a forma de uma região tridimensional  Suponha que a densidade de massa em
Suponha que a densidade de massa em  seja
seja 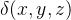 e que
e que 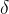 seja cont
seja cont nua em toda
nua em toda 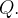 Seja
Seja 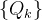 uma partição interior de
uma partição interior de 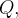 e seja
e seja 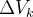 o volume de
o volume de 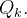 Se
Se 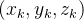 é um ponto de
é um ponto de 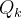 então a massa correspondente é aproximadamente igual a
então a massa correspondente é aproximadamente igual a 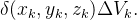 A massa do sólido é o limite de tais somas, isto é,
A massa do sólido é o limite de tais somas, isto é, 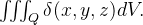
O momento em relação ao plano- da parte do sólido que corresponde a
da parte do sólido que corresponde a 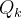 é aproximado por
é aproximado por 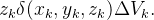 Somando e tomando o limite, obtemos o momento do sólido
Somando e tomando o limite, obtemos o momento do sólido  em relação ao plano
em relação ao plano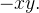 Analogamente, obtemos os momentos
Analogamente, obtemos os momentos 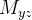 e
e 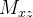 do sólido em relação aos planos
do sólido em relação aos planos  e
e 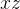 , respectivamente. Ou seja, temos
, respectivamente. Ou seja, temos
Momentos e centros de massa em três dimensões:
![\[ m=\iiint _{Q}\delta (x,y,z)dV. \]](images/img-0264.png) |
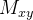 |
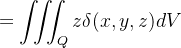 |
|||
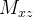 |
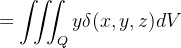 |
|||
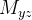 |
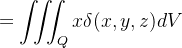 |
![\[ \overline{x}=\frac{M_{yz}}{m};\; \overline{y}=\frac{M_{xz}}{m};\; \overline{z}=\frac{M_{xy}}{m}\; \; \text {(\textbf{centro de massa})} \]](images/img-0271.png) |
Centróide: 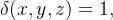 obtemos o centróide
obtemos o centróide 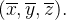
Um sólido tem a forma de um cilindro circular reto de raio da base 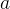 e altura
e altura  A densidade num ponto
A densidade num ponto 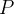 é diretamente proporcional à distância de uma das bases a
é diretamente proporcional à distância de uma das bases a 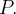 Ache o centro de massa.
Ache o centro de massa.
Sol.: No exemplo anterior, vimos que 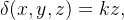 e obtivemos
e obtivemos 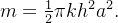
O centro de massa está no eixo- , de modo que basta achar
, de modo que basta achar 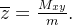 Além disso, pela simetria do sólido e pela forma de
Além disso, pela simetria do sólido e pela forma de 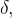 podemos calcular
podemos calcular  da seguinte forma:
da seguinte forma:
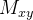 |
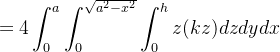 |
|||
 |
![$\displaystyle =4k\int _{0}^{a}\int _{0}^{\sqrt{a^{2}-x^{2}}}\left[ \frac{z^{3}}{3}\right] _{0}^{h}dydx $](images/img-0282.png) |
|||
 |
 |
|||
 |
![$\displaystyle =\frac{4}{3}kh^{3}\int _{0}^{a}\left[ y\right] _{0}^{\sqrt{a^{2}-x^{2}}}dx $](images/img-0284.png) |
|||
 |
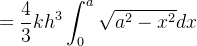 |
|||
 |
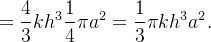 |
Da
![\[ \overline{z}=\frac{M_{xy}}{m}=\frac{\frac{1}{3}\pi kh^{3}a^{2}}{\frac{1}{2}\pi kh^{2}a^{2}}=\frac{2}{3}h. \]](images/img-0287.png) |
logo, o centro de massa é 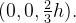
Um sólido tem a forma da região do primeiro octante delimitada pelo parabolóide 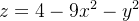 e os planos
e os planos 
 e
e 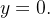 A densidade em
A densidade em 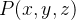 é proporcional à distância da origem a
é proporcional à distância da origem a 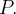 Estabeleça integrais iteradas para calcular
Estabeleça integrais iteradas para calcular 
Sol.: A densidade em  é
é  para algum
para algum 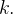 Temos que
Temos que
![\[ m=\int _{0}^{\frac{8}{5}}\int _{y/4}^{\sqrt{4-y^{3}}/3}\int _{0}^{4-9x^{2}-y^{2}}k(x^{2}+y^{2}+z^{2})^{1/2}dzdxdy \]](images/img-0295.png) |
![\[ M_{yz}=\int _{0}^{\frac{8}{5}}\int _{y/4}^{\sqrt{4-y^{3}}/3}\int _{0}^{4-9x^{2}-y^{2}}xk(x^{2}+y^{2}+z^{2})^{1/2}dzdxdy \]](images/img-0296.png) |
![\[ \overline{x}=\frac{M_{yz}}{m}. \]](images/img-0297.png) |
Se uma part cula de massa
cula de massa 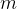 está no ponto
está no ponto 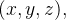 então sua distância ao eixo-
então sua distância ao eixo- é
é  e seu momento de inércia
e seu momento de inércia 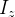 em relação ao eixo-
em relação ao eixo- define-se como
define-se como 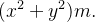 Da mesma forma, os momentos de inércia
Da mesma forma, os momentos de inércia 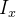 e
e 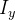 em relação aos eixos
em relação aos eixos  e
e 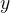 são
são 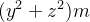 e
e 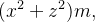 respectivamente. Para sólidos
respectivamente. Para sólidos 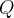 obtemos o seguinte.
obtemos o seguinte.
Momento de inércia de sólidos
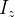 |
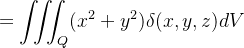 |
|||
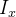 |
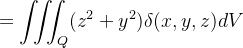 |
|||
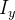 |
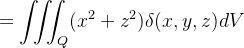 |
Ache o momento de inércia, em relação ao eixo de simetria, do sólido cil ndrico descrito no exemplo anterior.
ndrico descrito no exemplo anterior.
Sol.: Como 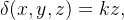 temos
temos
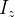 |
 |
|||
 |
![$\displaystyle =4k\int _{0}^{a}\int _{0}^{\sqrt{a^{2}-x^{2}}}(x^{2}+y^{2})\left[ \frac{z^{2}}{2}\right] _{0}^{h}dydx $](images/img-0314.png) |
|||
 |
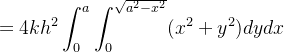 |
|||
 |
![$\displaystyle =2kh^{2}\int _{0}^{a}\left[ x^{2}y+\frac{1}{3}y^{3}\right] _{0}^{\sqrt{a^{2}-x^{2}}}dx $](images/img-0316.png) |
|||
 |
![$\displaystyle =2kh^{2}\int _{0}^{a}\left[ x^{2}\sqrt{a^{2}-x^{2}}+\frac{1}{3}\sqrt{(a^{2}-x^{2})^{3}}\right] $](images/img-0317.png) |
|||
 |
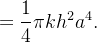 |
Um sólido homogêneo tem a forma da região 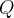 delimitada pelo cone
delimitada pelo cone 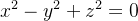 e o plano
e o plano 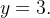 Estabeleça uma integral tripla para calcular seu momento de inércia em relação ao eixo-
Estabeleça uma integral tripla para calcular seu momento de inércia em relação ao eixo-
Sol.: Note que o traço do cone no plano- é o par de retas
é o par de retas 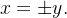 Denotando por
Denotando por 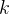 a densidade constante, temos
a densidade constante, temos
![\[ I_{y}=\int _{0}^{3}\int _{-y}^{y}\int _{-\sqrt{y^{2}-x^{2}}}^{\sqrt{y^{2}-x^{2}}}(x^{2}+z^{2})kdzdxdy. \]](images/img-0323.png) |