| Cálculo Diferencial e Integral 3 |
Se 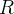 é uma região retangular do tipo
é uma região retangular do tipo
![\[ R=\left\{ (x,y):\ a\leq x\leq b,\ c\leq y\leq d\right\} \]](images/img-0046.png) |
então a integral de uma função  definida em
definida em 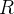 é dada por
é dada por
![\[ {\displaystyle \iint \limits _{R}} f(x,y)dA=\int _{a}^{b}\int _{c}^{d}f(x,y)dydx=\int _{a}^{b}\left[ \int _{c}^{d}f(x,y)dy\right] dx, \]](images/img-0047.png) |
ou
![\[ {\displaystyle \iint \limits _{R}} f(x,y)dA=\int _{c}^{d}\int _{a}^{b}f(x,y)dxdy=\int _{c}^{d}\left[ \int _{a}^{b}f(x,y)dx\right] dy. \]](images/img-0048.png) |
Calcule 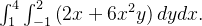
Solução: Por definição
 |
![$\displaystyle =\int _{1}^{4}\left[ 2xy+6x^{2}\left( \frac{y^{2}}{2}\right) \right] _{-1}^{2}dx $](images/img-0051.png) |
|||
 |
![$\displaystyle =\int _{1}^{4}\left[ \left( 4x+12x^{2}\right) -\left( -2x+3x^{2}\right) \right] dx $](images/img-0053.png) |
|||
 |
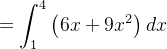 |
|||
 |
![$\displaystyle =\left[ 3x^{2}+3x^{3}\right] _{1}^{4}=234. $](images/img-0055.png) |
Calcule 
Solução: Temos que
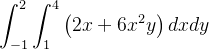 |
![$\displaystyle =\int _{-1}^{2}\left[ 2\frac{x^{2}}{2}+6\left( \frac{x^{3}}{3}\right) y\right] _{1}^{4}dy $](images/img-0058.png) |
|||
 |
![$\displaystyle =\int _{-1}^{2}\left[ \left( 16+128y\right) -\left( 1+2y\right) \right] dy $](images/img-0059.png) |
|||
 |
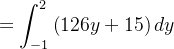 |
|||
 |
![$\displaystyle =\left[ 63y^{2}+15y\right] _{-1}^{2}=234. $](images/img-0061.png) |
Agora queremos integrar sobre regiões dos tipos abaixo. Damos a seguinte definição.
(i) ![$\int _{a}^{b}\int _{g_{1}(x)}^{g_{2}(x)}f(x,y)dydx=\int _{a}^{b}\left[ \int _{g_{1}(x)}^{g_{2}(x)}f(x,y)dy\right] dx$](images/img-0062.png)
(ii) ![$\int _{c}^{d}\int _{h_{1}(y)}^{h_{2}(y)}f(x,y)dxdy=\int _{c}^{d}\left[ \int _{h_{1}(y)}^{h_{2}(y)}f(x,y)dx\right] dy.$](images/img-0063.png)
Calcule 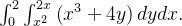
Solução: Por definição
![$\displaystyle \int _{0}^{2}\left[ \int _{x^{2}}^{2x}\left( x^{3}+4y\right) dy\right] dx $](images/img-0065.png) |
![$\displaystyle =\int _{0}^{2}\left[ x^{3}y+4\frac{y^{2}}{2}\right] _{x^{2}}^{2x}dx $](images/img-0066.png) |
|||
 |
![$\displaystyle =\int _{0}^{2}\left[ \left( x^{3}\left( 2x\right) +2(2x)^{2}\right) -\left( x^{3}x^{2}+2\left( x^{2}\right) ^{2}\right) \right] dx $](images/img-0067.png) |
|||
 |
![$\displaystyle =\int _{0}^{2}\left[ 8x^{2}-x^{5}\right] dx $](images/img-0068.png) |
|||
 |
![$\displaystyle =\left[ 8\frac{x^{3}}{3}-\frac{x^{6}}{6}\right] _{0}^{2}=\frac{32}{3}. $](images/img-0069.png) |
Calcule 
Solução: Temos que
 |
![$\displaystyle =\int _{1}^{3}2y\left[ \operatorname {sen}x\right] _{\frac{\pi }{6}}^{y^{2}}dy $](images/img-0072.png) |
|||
 |
![$\displaystyle =\int _{1}^{3}2y\left[ \operatorname {sen}y^{2}-\operatorname {sen}\frac{\pi }{6}\right] dy $](images/img-0073.png) |
|||
 |
 |
|||
 |
![$\displaystyle =\left[ -\cos y^{2}-\frac{y^{2}}{2}\right] _{1}^{3} $](images/img-0075.png) |
|||
 |
 |
Seja 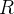 uma região do tipo
uma região do tipo 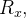 ou seja, uma região definida por
ou seja, uma região definida por
![\[ R_{x}=\left\{ \left( x,y\right) \in \mathbb {R}^{2}:g_{1}(x)\leq y\leq g_{2}(x),\ a\leq x\leq b\ \right\} \]](images/img-0078.png) |
ou do tipo 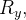 isto é, uma região definida por
isto é, uma região definida por
![\[ R_{x}=\left\{ \left( x,y\right) \in \mathbb {R}^{2}:h_{1}(y)\leq x\leq h_{2}(y),\ c\leq y\leq d\ \right\} \]](images/img-0080.png) |
então temos que
![\[ {\displaystyle \iint \limits _{R}} f(x,y)dA=\int _{a}^{b}\int _{g_{1}(x)}^{g_{2}\left( x\right) }f(x,y)dydx \]](images/img-0081.png) |
ou
![\[ {\displaystyle \iint \limits _{R}} f(x,y)dA=\int _{c}^{d}\int _{h_{1}(y)}^{h_{2}\left( y\right) }f(x,y)dxdy. \]](images/img-0082.png) |
Seja 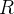 a região do plano-xy delimitada pelos gráficos de
a região do plano-xy delimitada pelos gráficos de  e
e  com
com  variando de
variando de 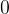 a
a  Calcule
Calcule 
Solução: Temos que
 |
![$\displaystyle =\int _{0}^{\frac{\pi }{4}}\int _{\operatorname {sen}x}^{\cos x}(y+1)dydx=\int _{0}^{\frac{\pi }{4}}\left[ \frac{y^{2}}{2}+y\right] _{\operatorname {sen}x}^{\cos x}dx $](images/img-0090.png) |
|||
 |
![$\displaystyle =\int _{0}^{\frac{\pi }{4}}\left[ \frac{\cos ^{2}x}{2}+\cos x-\frac{\operatorname {sen}^{2}x}{2}-\operatorname {sen}x\right] dx $](images/img-0091.png) |
|||
 |
![$\displaystyle =\left[ \frac{1}{4}\operatorname {sen}2x+\operatorname {sen}x+\cos x\right] _{0}^{\frac{\pi }{4}}=\sqrt{2}-\frac{3}{4}. $](images/img-0092.png) |