| Cálculo Diferencial e Integral 3 |
Considere a figura abaixo.
Temos um retângulo  . Dividimos
. Dividimos  em retângulos menores. A totalidade das subregiões retangulares fechadas inteiramente contidas em
em retângulos menores. A totalidade das subregiões retangulares fechadas inteiramente contidas em 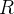 constitui uma particão interior de
constitui uma particão interior de 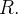 Designando por
Designando por 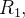
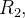
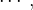
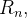 essas subregiões retangulares, então a particão interior é
essas subregiões retangulares, então a particão interior é 
 O comprimento da maior diagonal das
O comprimento da maior diagonal das 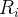 será denotada por
será denotada por  e chamada norma da particão
e chamada norma da particão 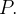 A área de
A área de 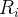 denotamos por
denotamos por 
Seja  uma funcão de duas variáveis definida numa região
uma funcão de duas variáveis definida numa região 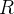 e
e 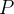

 uma particão de
uma particão de 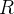 . Uma soma de Riemann de
. Uma soma de Riemann de  para
para 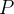 é qualquer soma da forma
é qualquer soma da forma
![\[ \sum _{i=1}^{n}f(u_{i},v_{i})\Delta A_{i} \]](images/img-0018.png) |
 está em
está em 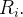
Sejam  uma função de duas variáveis definida numa região
uma função de duas variáveis definida numa região 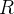 e
e 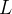 um número real. A afirmação
um número real. A afirmação
![\[ \lim _{\left\| P\right\| \rightarrow 0}\sum _{i=1}^{n}f(u_{i},v_{i})\Delta A_{i}=L \]](images/img-0022.png) |
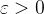 arbitrário, existe
arbitrário, existe  tal que se
tal que se 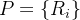 é uma partição interior de
é uma partição interior de 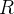 com
com 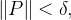 então
então ![\[ \left| \sum _{i=1}^{n}f(u_{i},v_{i})\Delta A_{i}-L\right| <\varepsilon \]](images/img-0027.png) |
 em
em 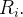
Seja  uma função de duas variáveis definida em
uma função de duas variáveis definida em 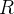 . A integral dupla de
. A integral dupla de  sobre
sobre 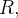 é dada por
é dada por
![\[ \iint _{R}f(x,y)dA=\lim _{\left\| P\right\| \rightarrow 0}\sum _{i=1}^{n}f(u_{i},v_{i})\Delta A_{i} \]](images/img-0029.png) |
Seja  cont
cont nua
nua  com
com  para todo
para todo  (região de definição de
(região de definição de  ). O volume do sólido compreendido entre o gráfico de
). O volume do sólido compreendido entre o gráfico de 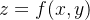 e acima de
e acima de 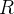 é
é
![\[ V={\displaystyle \iint \limits _{R}} f(x,y)dA. \]](images/img-0035.png) |
Se  em
em 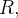 a integral dupla de
a integral dupla de  sobre
sobre 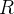 é o negativo do volume sólido situado acima do gráfico de
é o negativo do volume sólido situado acima do gráfico de  e sob a região
e sob a região 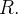
Seja  uma função integrável e
uma função integrável e  uma constante real qualquer. Temos que
uma constante real qualquer. Temos que
(i) 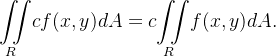
(ii) 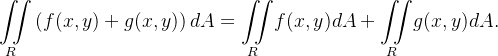
(iii) Se 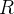 é a união de duas regiões não superpostas
é a união de duas regiões não superpostas 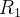 e
e  então
então
![\[ {\displaystyle \iint \limits _{R}} f(x,y)dA={\displaystyle \iint \limits _{R_{1}}} f(x,y)dA+{\displaystyle \iint \limits _{R_{2}}} f(x,y)dA. \]](images/img-0042.png) |
(iv) Se 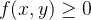 em
em  então
então 