| Séries e Equações Diferenciais Ordinárias |
I ) Seja 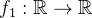 periódica de per
periódica de per odo
odo 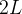 e definida por
e definida por 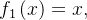 para
para 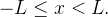 Como
Como 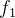 é
é  mpar, teremos uma série de senos cujos coeficientes são:
mpar, teremos uma série de senos cujos coeficientes são:
![\[ a_{n}=0;\ b_{n}=\dfrac {2}{L}{\displaystyle \int _{0}^{L}} x\operatorname{sen}\dfrac {n\pi x}{L}dx. \]](images/img-0859.png) |
fazendo a mudança de variável 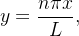 obtemos:
obtemos:
![\[ b_{n}=\dfrac {2}{L}{\displaystyle \int _{0}^{n\pi }} \dfrac {L}{n\pi }y\operatorname{sen}\left( y\right) \dfrac {L}{n\pi }dy=\dfrac {2L}{n^{2}\pi ^{2}}{\displaystyle \int _{0}^{n\pi }} y\operatorname{sen}\left( y\right) dy. \]](images/img-0861.png) |
Integrando por partes, temos
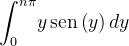 |
![$\displaystyle =\left[ -y\cos y\right] _{0}^{n\pi }+{\displaystyle \int _{0}^{n\pi }} \cos \left( y\right) dy $](images/img-0863.png) |
|||
 |
![$\displaystyle =-n\pi \cos \left( n\pi \right) -\left( 0\right) +\left[ \operatorname{sen}\left( y\right) \right] _{0}^{n\pi }=-n\pi \cos \left( n\pi \right) $](images/img-0864.png) |
Logo
![\[ b_{n}=\dfrac {2L}{n^{2}\pi ^{2}}\left( -n\pi \cos \left( n\pi \right) \right) \Rightarrow b_{n}=\dfrac {2L}{n\pi }\left( -\cos \left( n\pi \right) \right) , \]](images/img-0865.png) |
como
![\[ \ \left\{ \begin{array}[c]{l}\text {para\ \ }n\ \text {\'{\i }mpar, }\cos \left( n\pi \right) =-1\\ \text {para\ \ }n\text { par, }\cos \left( n\pi \right) =1 \end{array} \right. \]](images/img-0866.png) |
então
![\[ b_{n}=\dfrac {2L}{n\pi }\left( -1\right)^{n+1}. \]](images/img-0867.png) |
Portanto a série de Fourier da função 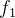 é:
é:
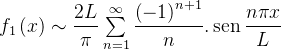
e seu gráfico é:
![\includegraphics[ height=2.2309in, width=3.9525in ]{Figura24.eps}](images/img-0869.png)
II ) Seja 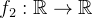 periódica de per
periódica de per odo
odo 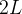 e definida por
e definida por
![\[ f_{2}\left( x\right) =\left\{ \begin{array}[c]{c}L-x,\text { para }0\leq x\leq L;\\ L+x,\text { para }-L\leq x\leq 0 \end{array} \right. \]](images/img-0871.png) |
Como 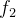 é uma função par, temos uma série de cossenos, cujos coeficientes são:
é uma função par, temos uma série de cossenos, cujos coeficientes são:
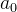 |
![$\displaystyle =\dfrac {2}{L}{\displaystyle \int _{0}^{L}} \left( L-x\right) dx=\frac{2}{L}\left[ Lx-\dfrac {x^{2}}{2}\right] _{0}^{L} $](images/img-0874.png) |
|||
 |
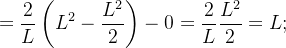 |
e
![\[ a_{n}=\dfrac {2}{L}{\displaystyle \int _{0}^{L}} \left( L-x\right) \cos \dfrac {n\pi x}{L}dx \]](images/img-0876.png) |
fazendo a mudança de variável 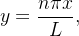 obtemos:
obtemos:
![\[ a_{n}=\dfrac {2}{L}{\displaystyle \int _{0}^{n\pi }} \left( L-\dfrac {L}{n\pi }y\right) \cos \left( y\right) \dfrac {L}{n\pi }dy \]](images/img-0877.png) |
![\[ =\dfrac {2}{L}{\displaystyle \int _{0}^{n\pi }} L\left( \dfrac {n\pi -y}{n\pi }\right) \cos \left( y\right) \dfrac {L}{n\pi }dy= \]](images/img-0878.png) |
![\[ =\dfrac {2L}{n^{2}\pi ^{2}}{\displaystyle \int _{0}^{n\pi }} \left( n\pi -y\right) \cos \left( y\right) dy \]](images/img-0879.png) |
Integrando por partes a integral acima, temos
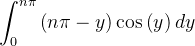 |
![$\displaystyle =\left[ \left( n\pi -y\right) \operatorname{sen}\left( y\right) \right] _{0}^{n\pi } $](images/img-0881.png) |
|||
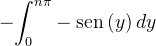 |
![$\displaystyle =0-0+\left[ -\cos \left( y\right) \right] _{0}^{n\pi } $](images/img-0883.png) |
|||
 |
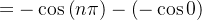 |
|||
 |
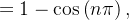 |
Logo,
![\[ a_{n}=\dfrac {2L}{n^{2}\pi ^{2}}\left( 1-\cos \left( n\pi \right) \right) \]](images/img-0886.png) |
como
![\[ \\ \left\{ \begin{array}[c]{l}\text {para \ }n\text {\ \ \'{\i }mpar, }\cos \left( n\pi \right) =-1\\ \text {para \ }n\text {\ \ par, }\cos \left( n\pi \right) =1 \end{array} \right. \]](images/img-0887.png) |
então
![\[ a_{n}=\dfrac {2L}{n^{2}\pi ^{2}}\left[ 1-\left( -1\right) ^{n}\right] \]](images/img-0888.png) |
ou seja,para 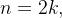 temos:
temos: 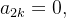
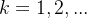 e para
e para 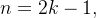 temos:
temos:
![\[ a_{2k-1}=\dfrac {2L}{\left( 2k-1\right) ^{2}\pi ^{2}}\left[ 1-\left( -1\right) \right] \Rightarrow a_{2k-1}=\dfrac {4L}{\left( 2k-1\right) ^{2}\pi ^{2}},\ k=1,2,... \]](images/img-0893.png) |
Portanto a série de Fourier da função 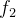 é:
é:
![\[ f_{2}\left( x\right) \sim \dfrac {L}{2}+\dfrac {4L}{\pi ^{2}}\sum \limits _{k=1}^{\infty }\dfrac {1}{\left( 2k-1\right) ^{2}}.\cos \dfrac {\left( 2k-1\right) \pi x}{L}. \]](images/img-0894.png) |
gráfico da função 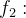
![\includegraphics[ height=2.041in, width=4.8032in ]{Figura23.eps}](images/img-0896.png)
Observe que, em virtude do Teorema de Fourier, o s mbolo
mbolo  pode ser substitu
pode ser substitu do por
do por  . Usando o Teorema de Fourier, para
. Usando o Teorema de Fourier, para 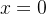 , obtemos:
, obtemos:
![\[ L-0=\dfrac {L}{2}+\dfrac {4L}{\pi ^{2}}\sum \limits _{k=1}^{\infty }\dfrac {1}{\left( 2k-1\right) ^{2}}, \]](images/img-0899.png) |
ou seja,
![\[ \dfrac {L}{2}=\dfrac {4L}{\pi ^{2}}\sum \limits _{k=1}^{\infty }\dfrac {1}{\left( 2k-1\right) ^{2}}\Rightarrow \dfrac {\pi ^{2}}{8}=\sum \limits _{k=1}^{\infty }\dfrac {1}{\left( 2k-1\right) ^{2}}=1+\dfrac {1}{3^{2}}+\dfrac {1}{5^{2}}+\dfrac {1}{7^{2}}+... \]](images/img-0900.png) |
III ) Seja 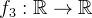 periódica de pr
periódica de pr odo
odo 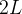 e definida por
e definida por 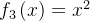 para
para 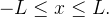 Como
Como 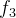 é par, teremos uma série de cossenos cujos coeficientes são:
é par, teremos uma série de cossenos cujos coeficientes são:
![\[ a_{0}=\dfrac {2}{L}{\displaystyle \int _{0}^{L}} x^{2}dx=\dfrac {2}{L}\left[ \dfrac {x^{3}}{3}\right] _{0}^{L}=\dfrac {2}{L}\left( \dfrac {L^{3}}{3}\right) -0=2\dfrac {L^{2}}{3}; \]](images/img-0905.png) |
![\[ a_{n}=\dfrac {2}{L}{\displaystyle \int _{0}^{L}} x^{2}\cos \dfrac {n\pi x}{L}dx. \]](images/img-0906.png) |
fazendo a mudança de variável 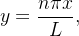 obtemos:
obtemos:
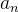 |
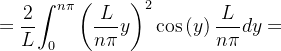 |
|||
 |
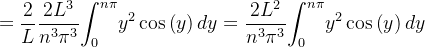 |
Integrando por partes, temos
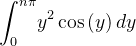 |
![$\displaystyle =\left[ y^{2}\operatorname{sen}\left( y\right) \right] _{0}^{n\pi }-{\displaystyle \int _{0}^{n\pi }} 2y\operatorname{sen}\left( y\right) dy $](images/img-0911.png) |
|||
 |
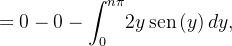 |
da ,
,
![\[ a_{n}=-\dfrac {4L^{2}}{n^{3}\pi ^{3}}{\displaystyle \int _{0}^{n\pi }} y\operatorname{sen}\left( y\right) dy \]](images/img-0913.png) |
Integrando novamente por partes, obtemos
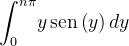 |
![$\displaystyle =\left[ -y\cos \left( n\pi \right) \right] _{0}^{n\pi }-{\displaystyle \int _{0}^{n\pi }} -\cos ydy $](images/img-0914.png) |
|||
 |
![$\displaystyle =-n\pi \cos \left( n\pi \right) -0+\left[ \operatorname{sen}y\right] _{0}^{n\pi } $](images/img-0915.png) |
|||
 |
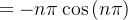 |
Logo,
![\[ a_{n}=-\dfrac {4L^{2}}{n^{3}\pi ^{3}}\left[ -n\pi \cos \left( n\pi \right) \right] =\dfrac {4L^{2}}{n^{3}\pi ^{3}}\left[ \cos \left( n\pi \right) \right] =\dfrac {4L^{2}}{n^{2}\pi ^{2}}\left( -1\right) ^{n} \]](images/img-0917.png) |
Portanto a série de Fourier da função 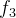 é:
é:
![\[ f_{3}\left( x\right) \sim \dfrac {L^{2}}{3}+\dfrac {4L^{2}}{\pi ^{2}}\sum \limits _{n=1}^{\infty }\dfrac {\left( -1\right) ^{n}}{n^{2}}\cos \dfrac {n\pi x}{L}. \]](images/img-0918.png) |
O gráfico da função 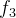 é dado pela figura 4.5.
é dado pela figura 4.5.
![\includegraphics[ height=2.2528in, width=4.8308in ]{Figura12.eps}](images/img-0919.png)
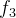
Observe que, de fato, tem-se  em vez de
em vez de  , como consequência do teorema de Fourier. Usando o Teorema de Fourier para
, como consequência do teorema de Fourier. Usando o Teorema de Fourier para 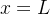 , obtemos:
, obtemos:
![\[ L^{2}=\dfrac {L^{2}}{3}+\dfrac {4L^{2}}{\pi ^{2}}\sum \limits _{n=1}^{\infty }\dfrac {1}{n^{2}}, \]](images/img-0921.png) |
pois 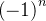 e
e 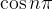 sempre terão o mesmo sinal e assim, pela multiplicação dos dois termos, sempre teremos
sempre terão o mesmo sinal e assim, pela multiplicação dos dois termos, sempre teremos 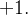
Ou seja,
![\[ L^{2}-\dfrac {L^{2}}{3}=\dfrac {4L^{2}}{\pi ^{2}}\sum \limits _{n=1}^{\infty }\dfrac {1}{n^{2}}\Rightarrow \dfrac {2L^{2}}{3}=\dfrac {4L^{2}}{\pi ^{2}}\sum \limits _{n=1}^{\infty }\dfrac {1}{n^{2}}\Rightarrow \]](images/img-0925.png) |
![\[ \Rightarrow \dfrac {\pi ^{2}}{6}=\sum \limits _{n=1}^{\infty }\dfrac {1}{n^{2}}=1+\dfrac {1}{2^{2}}+\dfrac {1}{3^{2}}+\dfrac {1}{4^{2}}+... \]](images/img-0926.png) |