| Séries e Equações Diferenciais Ordinárias |
Theorem 61 (Teste da Razão). Consideremos uma série se se se  com e seja
com e seja 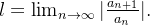
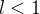 então a série
então a série  converge absolutamente.
converge absolutamente. 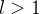 ou
ou  então
então  diverge.
diverge. 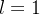 nada se pode concluir.
nada se pode concluir.
Se 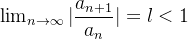 então existe um número real
então existe um número real 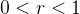 tal que
tal que
![\[ |\dfrac {a_{n+1}}{a_ n}|<r, \, \, \forall n>n_0 \]](images/img-0463.png) |
![\[ |a_{n_0+k}|\leq r^ k |a_{n_0}|, \, \, \forall k\geq 1 \]](images/img-0464.png) |
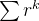 é convergente então
é convergente então 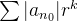 também converge e
também converge e 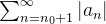 converge pelo teste de comparação, logo,
converge pelo teste de comparação, logo, 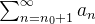 converge absolutamente, o que implica que
converge absolutamente, o que implica que 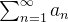 converge absolutamente (um número finito de termos não altera a convergência ou divergência da série). Se, por outro lado,
converge absolutamente (um número finito de termos não altera a convergência ou divergência da série). Se, por outro lado, 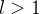 , então
, então 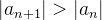 e se,
e se, 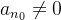 para algum
para algum 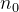 então,
então, 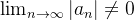 o que nos dá
o que nos dá 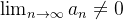 . Logo,
. Logo,  diverge (teste do n-ésimo termo).
diverge (teste do n-ésimo termo). Example 62. Considere a série as séries 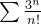 e
e 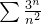 analise sobre a convergência ou divergência dessas séries.
analise sobre a convergência ou divergência dessas séries.
Solução: Pelo teste da razão, temos
![\[ \lim _{n\to \infty } \dfrac {3^{n+1}}{(n+1)!}\dfrac {n!}{3^ n}=\lim _{n\to \infty } \dfrac {3}{n+1}=0<1 \]](images/img-0475.png) |
então a série 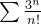 converge pelo teste da razão. E como
converge pelo teste da razão. E como
![\[ \lim _{n\to \infty } \dfrac {3^{n+1}}{(n+1)^2}\dfrac {n^2}{3^ n}=3>1 \]](images/img-0476.png) |
então a série 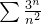 diverge pelo teste da razão.
diverge pelo teste da razão.
Example 63. Considere a série 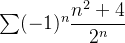 ela converge ou diverge?
ela converge ou diverge?
Solução: Usando o teste da razão temos
![\[ \lim _{n\to \infty } |\frac{a_{n+1}}{a_ n}|=\lim _{n\to \infty } \left|\dfrac {(-1)^{n+1} [(n+1)^2 +4]}{2^{n+1}}\dfrac {2^ n}{(-1)^ n (n^2+4)}\right|=\lim _{n\to \infty }\dfrac {1}{2}\displaystyle (\dfrac {n^2+2n+5}{n^2+4})=\dfrac {1}{2}<1 \]](images/img-0478.png) |
o que implica que a série converge.
Theorem 64 (Teste da Raíz). Seja se se se  uma série numérica. Seja
uma série numérica. Seja ![$\lim _{n\to \infty } \sqrt[n]{|a_ n|}=l$](images/img-0479.png) . Temos que
. Temos que
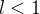 então
então  converge absolutamente.
converge absolutamente. 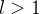 então
então  diverge.
diverge. 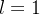 nada se conclui.
nada se conclui.
Suponha 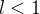 então existe
então existe 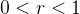 tal que
tal que
![\[ \sqrt[n]{|a_ n|}<r, \, \, \, \forall n>n_0 \]](images/img-0480.png) |
![\[ |a_ n|<r^ n, \, \, \, \forall n>n_0 \]](images/img-0481.png) |
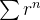 converge segue que
converge segue que 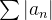 converge e, portanto,
converge e, portanto,  converge absolutamente. Por outro lado, se
converge absolutamente. Por outro lado, se 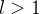 então existe
então existe 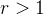 tal que
tal que ![\[ \sqrt[n]{|a_ n|}>r, \, \, \, \forall n>n_0 \]](images/img-0484.png) |
![\[ |a_ n|>r^ n, \, \, \, \forall n>n_0 \]](images/img-0485.png) |
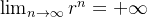 então
então 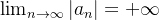 o que implica
o que implica  diverge (Por quê?).
diverge (Por quê?). Example 65. Considere a série 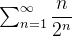 . Pelo teste da raíz:
. Pelo teste da raíz: ![$\lim _{n\to \infty } \sqrt[n]{\dfrac {n}{2^ n}}=\lim _{n\to \infty } \dfrac {\sqrt[n]{n}}{2}=\dfrac {1}{2}<1$](images/img-0489.png) . Logo,
. Logo, 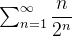 converge absolutamente.
converge absolutamente.
Example 66. A série 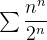 diverge pois, usando o teste da raíz, temos que
diverge pois, usando o teste da raíz, temos que ![$\lim _{n\to \infty } \sqrt[n]{\dfrac {n^ n}{2^ n}}=\lim _{n\to \infty } \dfrac {n}{2}=+\infty $](images/img-0491.png) .
.
Example 67. A série 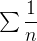 diverge e a série
diverge e a série 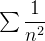 convergente mas
convergente mas ![$\lim _{n\to \infty } \sqrt[n]{\dfrac {1}{n}}=1,$](images/img-0492.png) e o limite
e o limite ![$\lim _{n \to \infty } \sqrt[n]{\dfrac {1}{n^2}}=\lim _{n\to \infty } \dfrac {1}{\sqrt[n]{n^2}}=\lim _{n \to \infty } \dfrac {1}{n^{2/n}}=1.$](images/img-0493.png) Se usarmos o teste da razão para essas mesmas séries obtemos resultados semelhantes do limite, ou seja, o limite será igual a
Se usarmos o teste da razão para essas mesmas séries obtemos resultados semelhantes do limite, ou seja, o limite será igual a 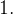 Por isso, quando
Por isso, quando 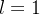 o resultado é inconclusivo, pois a série tanto pode convergir como divergir.
o resultado é inconclusivo, pois a série tanto pode convergir como divergir.