1.1.1 Indução Matemática

Se uma propriedade qualquer P vale para 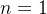$n=1$ e supomos ela válida para 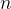$n$ e provamos que P vale para 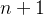$n+1$ , então P vale para todo 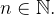$n\in \mathbb {N}.$ Esse é o princípio de Indução Matemática.

Example 7. Seja 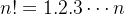$n!=1.2.3\cdots n$ . Provemos que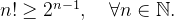 $n!\geq 2^{n-1}, \quad \forall n\in \mathbb {N}.$

De fato, sabemos que 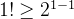$1!\geq 2^{1-1}$ , assim essa propriedade vale para 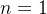$n=1$ , suponha que ela vale para 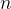$n$ , isto é, 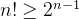$n!\geq 2^{n-1}$ . Considere agora, 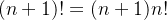$(n+1)!=(n+1)n!$ , desse modo,

$(n+1)!=(n+1)n!\geq (n+1)2^{n-1}\geq (1+1)2^{n-1}=2^ n$

Logo, a propriedade vale para 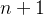$n+1$ , e, portanto, vale para todo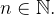 $n\in \mathbb {N}.$

Example 8. Provemos que 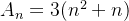$A_ n=3(n^2 +n)$ é divisível por 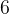$6$ , para todo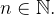 $n\in \mathbb {N}.$

De fato, temos que para 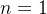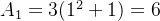$n=1$ $A_1=3(1^2+1)=6$ que divide 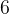$6$ . Suponha que 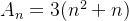$A_ n=3(n^2+n)$ seja divisível por 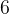$6$ , isto é, existe 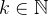$k\in \mathbb {N}$ tal que 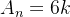$A_ n=6k$ . Agora considere,

$A_{n+1}=3[(n+1)^2+(n+1)]=3(n^2+n)+3[(2n+1)+1]=6k+6(n+1)$

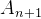Logo, $A_{n+1}$ é divisível por 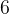$6$ . Por indução, essa propriedade vale para todo $n\in \mathbb {N}.$