| Séries e Equações Diferenciais Ordinárias |
Uma sequência numérica é uma função 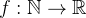 que a cada número natural
que a cada número natural 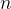 associa um número real
associa um número real 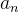 , isto é,
, isto é, 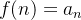 . O termo
. O termo 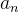 diz-se o n-ésimo termo da sequência ou termo geral da sequência.
diz-se o n-ésimo termo da sequência ou termo geral da sequência.
Example 1.
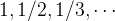 ,
, 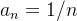
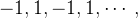
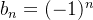
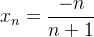 é o termo geral da sequência
é o termo geral da sequência 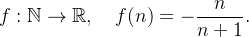
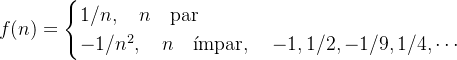
Se considerarmos 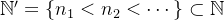 a restrição de
a restrição de 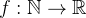 a
a 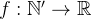 é chamada de subsequência ou subsucessão da sequência original
é chamada de subsequência ou subsucessão da sequência original 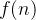 .
.
Example 2. A sequência A sequência
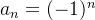 tem como subsequências
tem como subsequências 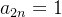 e
e 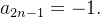
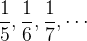 é uma subsequência da sequência
é uma subsequência da sequência 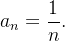 Observe que poderíamos denotá-la por
Observe que poderíamos denotá-la por 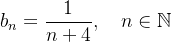 ou ainda
ou ainda 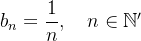 onde
onde 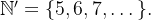
De forma geral, fixado 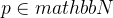 , então a sequência com termo geral
, então a sequência com termo geral 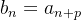 é uma subsequência de
é uma subsequência de 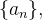 onde consideramos para domínio o subconjunto
onde consideramos para domínio o subconjunto 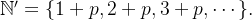
Definition 3. Uma sequência 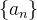 é dita limitada superiormente quando existir um número real
é dita limitada superiormente quando existir um número real 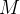 , denominado cota superior da sequência que satisfaz
, denominado cota superior da sequência que satisfaz
![\[ a_ n\leq M, \quad \forall n\in \mathbb {N} \]](images/img-0029.png)
Definition 4. Uma sequência 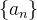 é dita limitada inferiormente quando existir um número real
é dita limitada inferiormente quando existir um número real 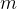 , denominado cota inferior da sequência que satisfaz
, denominado cota inferior da sequência que satisfaz
![\[ a_ n\geq m, \quad \forall n\in \mathbb {N} \]](images/img-0031.png)
Definition 5. Uma sequência 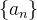 é dita limitada quando ela for limitada superiormente e inferiormente, isto é, quando existir uma constante positiva
é dita limitada quando ela for limitada superiormente e inferiormente, isto é, quando existir uma constante positiva  , tal que
, tal que
![\[ |a_ n|\leq C, \quad \forall n\in \mathbb {N} \]](images/img-0033.png)
É claro que se 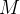 for uma cota superior de uma dada sequência
for uma cota superior de uma dada sequência 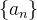 , então qualquer número real maior do que
, então qualquer número real maior do que 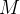 também será cota superior da sequência
também será cota superior da sequência 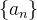 . A menor dessas cotas superiores será chamada de supremo da sequência
. A menor dessas cotas superiores será chamada de supremo da sequência 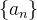 e a denotamos por sup
e a denotamos por sup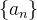 . Analogamente, definimos o ínfimo da sequência
. Analogamente, definimos o ínfimo da sequência 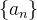 e denotamos por inf
e denotamos por inf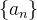 , que é a maior das cotas inferiores da sequência. Note que para cada
, que é a maior das cotas inferiores da sequência. Note que para cada 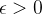 o número real
o número real 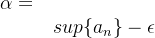 é menor que o supremo da sequência
é menor que o supremo da sequência 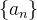 e, portanto, não pode ser cota superior dessa sequência, por esse motivo, deve existir um
e, portanto, não pode ser cota superior dessa sequência, por esse motivo, deve existir um 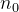 tal que
tal que 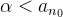 . Para o ínfimo ocorre fato análogo, ou seja, sendo
. Para o ínfimo ocorre fato análogo, ou seja, sendo 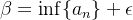 existe algum termo da sequência tal que
existe algum termo da sequência tal que 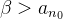 .
.
Example 6. A sequência A sequência A sequência A sequência A sequência
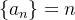 é limitada inferiormente, mas não é limitada superiormente,
é limitada inferiormente, mas não é limitada superiormente, 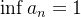 .
. 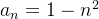 é limitada superiormente, mas não é limitada inferiormente e
é limitada superiormente, mas não é limitada inferiormente e 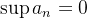 .
. 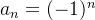 é limitada, sendo
é limitada, sendo 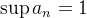 e
e 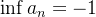 .
. 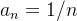 é limitada,
é limitada, 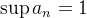 e
e 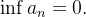
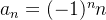 não é limitada superiormente nem inferiormente.
não é limitada superiormente nem inferiormente.