1.5 Imunidade diminui com o tempo

Vamos supor que depois de um tempo a imunidade das pessoas que tiveram a gripe tenha baixado e elas estejam sujeitas a pegarem a gripe novamente, isto é, elas se tornaram suscetíveis à doença novamente. Isto significa que houve um transporte do estado de quem estava em 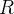$R$ para os que estavam em $S$ .

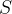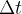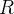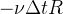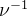O modelo que envolve a perda de imunidade é semelhante ao modelo de espalhamento da doença: a quantidade de pessoas perdendo imunidade é proporcional a quantidade de pacientes recuperados no intervalo de tempo $\Delta t$ . Nós podemos escrever a perda na categoria $R$ como $-\nu \Delta t R$ onde $\nu ^{-1}$ é tipicamente o tempo que se leva para perder a imunidade.

A perda em 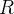$R$ é um ganho em 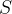$S$ . O modelo então se torna:

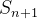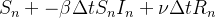$\displaystyle S_{n+1}$	$\displaystyle =$	$\displaystyle S_ n+ -\beta \Delta t S_ n I_ n+\nu \Delta t R_ n$	(26)
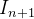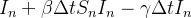$\displaystyle I_{n+1}$	$\displaystyle =$	$\displaystyle I_ n+\beta \Delta t S_ n I_ n-\gamma \Delta t I_ n$	(27)
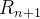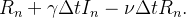$\displaystyle R_{n+1}$	$\displaystyle =$	$\displaystyle R_ n+\gamma \Delta t I_ n-\nu \Delta t R_ n.$	(28)

dividindo por 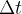$\Delta t$ e fazendo 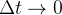$\Delta t \to 0$ obtemos

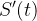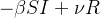$\displaystyle S’(t)$	$\displaystyle =$	$\displaystyle -\beta S I+\nu R$	(29)
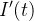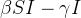$\displaystyle I’(t)$	$\displaystyle =$	$\displaystyle \beta S I-\gamma I$	(30)
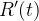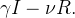$\displaystyle R’(t)$	$\displaystyle =$	$\displaystyle \gamma I-\nu R.$	(31)

Este sistema pode ser resolvido pelo mesmo método usado para resolver o sistema SIR. Somente uma modificação é necessária somando $\nu R[n]$ a $S[n+1]$ e subtraindo essa mesma quantidade de $R[n+1]$ .

for n in range(Nt):

S[n+1] = S[n]+ -beta*dt*S[n] I[n]+nu*dt*R[n]
I[n+1] = I[n]+beta Delta t S[n] I[n]-gamma*dt*I[n]
R[n+1] = R[n]+gamma*dt*I[n]-nu*dt *R[n]

Configurando 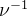$\nu ^{-1}$ para 50 dias, reduzindo 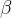$\beta$ por um fator de 4 comparado com o exemplo anterior ( 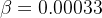$\beta =0.00033$ ) e simulando para 300 dias dá um comportamento oscilatório nas categorias, como retratada na figura 3 .

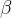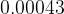É fácil brincar com os parâmetros e ver como eles afetam a disseminação da doença. Por exemplo, fazendo a doença se espalhar um pouquinho mais efetivamente (cresça $\beta$ para $0.00043$ ) e crescendo o tempo médio da perda de imunidade para 90 dias leva a outras oscilações, veja a figura 4.

$\includegraphics[scale=0.5]{imuncai.png}$

Figure 3: Incluindo perda de Imunidade

$\includegraphics[scale=0.5]{imundim.png}$

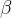Figure 4: Crescendo $\beta$ comparado à fig. 3