| Estudo Numérico de algumas EDOs |
Vamos estender esse modelo para incluir também a vacinação. Para este fim, pode ser útil rastrear os que se vacinaram e os que não. Portanto, vamos introduzir uma quarta categoria, 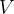 , para aquelas que tiveram sucesso na vacinação.
, para aquelas que tiveram sucesso na vacinação.
Além disso, vamos assumir que num certo intervalo de tempo 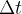 , a fração
, a fração 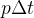 da categoria
da categoria 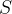 está sujeita ao sucesso da vacinação. Isto significa que no tempo
está sujeita ao sucesso da vacinação. Isto significa que no tempo 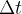 ,
, 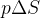 pessoas saem de
pessoas saem de 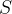 para a categoria
para a categoria 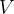 . Desde que as pessoas vacinadas não podem ter a doença, então não há impacto nas categorias
. Desde que as pessoas vacinadas não podem ter a doença, então não há impacto nas categorias 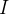 e
e 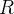 .
.
A nova equação diferencial estendida com a 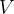 será:
será:
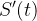 |
 |
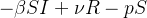 |
(32) | ||
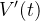 |
 |
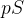 |
(33) | ||
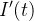 |
 |
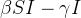 |
(34) | ||
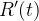 |
 |
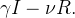 |
(35) |
Vamos nos referir a esse modelo como o modelo SIRV. A nova equação para 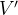 não oferece nenhuma dificuldade quando usamos o método numérico. Em um esquema de Euler avançado simplesmente acrescentamos a fórmula:
não oferece nenhuma dificuldade quando usamos o método numérico. Em um esquema de Euler avançado simplesmente acrescentamos a fórmula:
![\[ V_{n+1}=V_ n + p \Delta t S_ n \]](images/img-0135.png) |
O programa precisa guardar 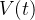 numa matriz adicional
numa matriz adicional 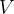 , e comando plot pode ser estendido com mais um argumento para
, e comando plot pode ser estendido com mais um argumento para 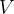 verso
verso 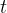 . Usando
. Usando 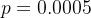 e
e 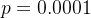 como valores para a eficiência da vacinação, o efeito da vacinação é visto pela figura 5.
como valores para a eficiência da vacinação, o efeito da vacinação é visto pela figura 5.
![\includegraphics[scale=0.38]{vacinp5.png}](images/img-0139.png)
![\includegraphics[scale=0.38]{vacinp1.png}](images/img-0140.png)
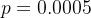 (esquerda) e
(esquerda) e 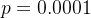 (direita)
(direita)![\includegraphics[scale=0.5]{campanha.png}](images/img-0141.png)
Como modelar uma campanha de vacinação? Imagine que depois de 6 dias do surto da doença, uma Estação de Saúde local inicialize uma campanha de vacinação. Eles alcançam muitas pessoas, digamos 10 vezes mais que o período de vacinação comum. Se a campanha dura 10 dias devemos então ter
![\[ p(t)= \begin{cases} 0.005, \quad 6.24\leq t \leq 15.24 \\ 0, \quad \mbox{para outros valores} \end{cases} \]](images/img-0142.png) |
Note que devemos multiplicar o valor de 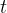 por 24 porque
por 24 porque 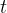 é medido em horas e não em dias. No sistema de equações diferencias,
é medido em horas e não em dias. No sistema de equações diferencias, 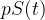 deve ser trocado por
deve ser trocado por 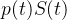 e neste caso, obtemos um sistema de equações diferenciais com um termo que é descontínuo.
e neste caso, obtemos um sistema de equações diferenciais com um termo que é descontínuo.
Isto é um grande desafio matemático, mas no tratamento numérico, ele fica fácil de tratar. Existem dois modos de implementar o coeficiente descontínuo 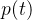 : através de uma função, ou através de uma matriz. a função de aproximação é mais fácil:
: através de uma função, ou através de uma matriz. a função de aproximação é mais fácil:
def p(t):
return 0.005 if (6.24<t<15.24) else 0
Na alteração do código nas array 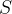 e
e 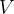 obtemos o termo
obtemos o termo ![$p[t_ n] S[n]$](images/img-0146.png) . Podemos também fazer
. Podemos também fazer 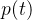 ser uma matriz, alocamos uma matriz
ser uma matriz, alocamos uma matriz 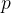 de comprimento
de comprimento 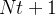 e achar os índices correspondentes aos 6 e 15 dias. Esses índices são achados do ponto do tempo dividido por
e achar os índices correspondentes aos 6 e 15 dias. Esses índices são achados do ponto do tempo dividido por 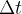 .
.
Isto é, p =zeros(Nt+1)
start-index=6.24/dt
stop-index=15.24/dt
p[star-index:stop-index]=0.005
O termo 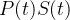 no mudança da equação em
no mudança da equação em 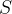 e
e 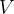 simplesmente torna-se
simplesmente torna-se ![$p[n]S[n]$](images/img-0149.png) .
.