| Cálculo Diferencial e Integral 3 |
Fluxo de um campo sobre uma superf cie fechada
cie fechada  que é fronteira de uma região
que é fronteira de uma região 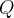 em três dimensões.
em três dimensões.
Teorema de Gauss. Seja 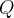 uma região em três dimensões delimitadas por uma superf
uma região em três dimensões delimitadas por uma superf cie fechada
cie fechada 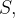 e denotemos por
e denotemos por  o vetor normal unitário exterior a
o vetor normal unitário exterior a  em
em 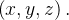 Se
Se 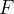 é uma função vetorial com derivadas parciais cont
é uma função vetorial com derivadas parciais cont nuas em
nuas em 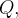 então
então
![\[ {\displaystyle \iint \limits _{S}} \mathbf{F}\cdot \mathbf{\eta }\text { }dS={\displaystyle \iiint \limits _{Q}} \nabla \cdot \mathbf{F\ }dV. \]](images/img-1259.png) |
Demonstração: Se  então o teorema de Gauss diz
então o teorema de Gauss diz
![\[ {\displaystyle \iint \limits _{S}} \left( M\mathbf{i}\cdot \mathbf{\eta }+N\mathbf{j}\cdot \mathbf{\eta }+P\mathbf{k}\cdot \mathbf{\eta }\right) dS={\displaystyle \iiint \limits _{Q}} \left( \frac{\partial M}{\partial x}+\frac{\partial N}{\partial y}+\frac{\partial P}{\partial z}\right) dV. \]](images/img-1261.png) |
Para provar esta igualdade é suficiente mostrar que
![\[ {\displaystyle \iint \limits _{S}} M\mathbf{i}\cdot \mathbf{\eta \ }dS={\displaystyle \iiint \limits _{Q}} \frac{\partial M}{\partial x}dV \]](images/img-1262.png) |
![\[ {\displaystyle \iint \limits _{S}} N\mathbf{j}\cdot \mathbf{\eta }\ dS={\displaystyle \iiint \limits _{Q}} \frac{\partial N}{\partial y}dV \]](images/img-1263.png) |
![\[ {\displaystyle \iint \limits _{S}} P\mathbf{k}\cdot \mathbf{\eta \ }dS={\displaystyle \iiint \limits _{Q}} \frac{\partial P}{\partial z}dV. \]](images/img-1264.png) |
Vamos provar a terceira igualdade.
 é a superf
é a superf cie de uma região
cie de uma região 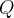 entre os gráficos de
entre os gráficos de  e
e  e acima de uma região
e acima de uma região  do plano-
do plano-

Sobre  o componente
o componente 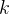 de
de  é zero e
é zero e  Assim
Assim  e podemos escrever
e podemos escrever
![\[ {\displaystyle \iint \limits _{S}} P\mathbf{k}\cdot \mathbf{\eta \ }dS={\displaystyle \iint \limits _{S_{1}}} P\mathbf{k}\cdot \mathbf{\eta \ }dS+{\displaystyle \iint \limits _{S_{3}}} P\mathbf{k}\cdot \mathbf{\eta \ }dS \]](images/img-1271.png) |
Para achar uma normal unitária (superior) a  fazemos
fazemos
![\[ g_{1}(x,y,z)=z-u\left( x,y\right) \]](images/img-1273.png) |
e calculamos
![\[ \mathbf{\eta }=\frac{\nabla g_{1}}{\left\Vert \nabla g_{1}\right\Vert }=\frac{-u_{x}\left( x,y\right) \mathbf{i}-u_{y}\left( x,y\right) \mathbf{j}+\mathbf{k}}{\sqrt{1+u_{x}^{2}+u_{y}^{2}}} \]](images/img-1274.png) |
Logo,  Assim, se
Assim, se  e
e  então
então
![\[ {\displaystyle \iint \limits _{S_{1}}} P\mathbf{k}\cdot \mathbf{\eta \ }dS={\displaystyle \iint \limits _{R}} P\left( x,y,u\left( x,y\right) \right) dA. \]](images/img-1278.png) |
Em 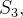 fazemos
fazemos
![\[ g_{2}\left( x,y,z\right) =z-v\left( x,y\right) \]](images/img-1280.png) |
e da
![\[ \mathbf{\eta }=\frac{\nabla g_{2}}{\left\Vert \nabla g_{2}\right\Vert }=\frac{v_{x}\left( x,y\right) \mathbf{i}+v_{y}\left( x,y\right) \mathbf{j}-\mathbf{k}}{\sqrt{1+v_{x}^{2}+v_{y}^{2}}}\ \left( \text { normal unit\'{a}ria inferior}\right) \]](images/img-1281.png) |
Aplicando as integrais sobre superf cies obtemos
cies obtemos
![\[ {\displaystyle \iint \limits _{S_{2}}} P\mathbf{k}\cdot \mathbf{\eta }dS=-{\displaystyle \iint \limits _{R}} P\left( x,y,v\left( x,y\right) \right) dA. \]](images/img-1282.png) |
Somando as integrais de fluxo sobre  e
e 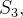 temos
temos
 |
![$\displaystyle ={\displaystyle \iint \limits _{R}} \left[ P\left( x,y,u\left( x,y\right) \right) -P\left( x,y,v\left( x,y\right) \right) \right] dA $](images/img-1285.png) |
|||
 |
![$\displaystyle ={\displaystyle \iint \limits _{R}} \left[ \int _{v\left( x,y\right) }^{u\left( x,y\right) }\frac{\partial P}{\partial z}dz\right] dA={\displaystyle \iiint \limits _{Q}} \frac{\partial P}{\partial z}dV. $](images/img-1286.png) |
Analogamente o temos o resultado:
![\[ {\displaystyle \iint \limits _{S}} M\mathbf{i}\cdot \mathbf{\eta \ }dS={\displaystyle \iiint \limits _{Q}} \frac{\partial M}{\partial x}dV,\ {\displaystyle \iint \limits _{S}} N\mathbf{j}\cdot \mathbf{\eta }\ dS={\displaystyle \iiint \limits _{Q}} \frac{\partial N}{\partial y}dV. \]](images/img-1287.png) |
Exemplo 1: Seja 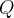 a região delimitada pelo cilindro circular reto
a região delimitada pelo cilindro circular reto  e pelos planos
e pelos planos  e
e  Denotemos por
Denotemos por  a superf
a superf cie de
cie de  Se
Se 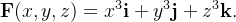 Use o Teorema de Gauss para calcular
Use o Teorema de Gauss para calcular 

Solução: Como
![\[ \operatorname {div}F=3x^{2}+3y^{2}+3z^{2}=3\left( x^{2}+y^{2}+z^{2}\right) \]](images/img-1293.png) |
temos
![\[ {\displaystyle \iint \limits _{S}} \mathbf{F}\cdot \mathbf{\eta }dS=3{\displaystyle \iiint \limits _{Q}} \left( x^{2}+y^{2}+z^{2}\right) dV \]](images/img-1294.png) |
Calculando em coordenadas cilindricas
 |
![$\displaystyle =3\int _{0}^{2\pi }\int _{0}^{2}\int _{0}^{3}\left( r^{2}+z^{2}\right) rdzdrd\theta =3\int _{0}^{2\pi }\int _{0}^{2}\left[ r^{2}z+\frac{z^{3}}{3}\right] _{0}^{3}rdrd\theta $](images/img-1296.png) |
|||
 |
![$\displaystyle =3\int _{0}^{2\pi }\int _{0}^{2}\left( 3r^{2}+9\right) rdrd\theta =3\int _{0}^{2\pi }\left[ \frac{3}{4}r^{4}+9\frac{r^{2}}{2}\right] _{0}^{2}d\theta =90\left[ \theta \right] _{0}^{2\pi }=180\pi . $](images/img-1297.png) |
Exemplo 2: Seja 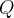 a região delimitada pelo cilindro
a região delimitada pelo cilindro  pelo plano
pelo plano 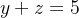 e pelos planos
e pelos planos  e
e  Seja
Seja  a superf
a superf cie de
cie de 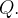 Se
Se 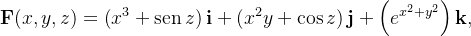 calcule
calcule 

Solução: Por Gauss
 |
 |
|||
 |
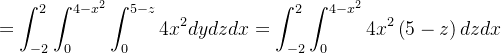 |
|||
 |
![$\displaystyle =\int _{-2}^{2}\left[ 20x^{2}z-4x^{2}\frac{z^{2}}{2}\right] _{0}^{4-x^{2}}dx=\int _{-2}^{2}\left( 48x^{2}-4x^{4}-2x^{6}\right) dx $](images/img-1304.png) |
|||
 |
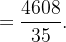 |